같은 문제집이라도 사람마다 푸는 방식이 다르고 학습된 결과도 다릅니다. 딥러닝 모델의 학습도 비슷합니다. 케라스에서는 모델을 학습시킬 때 fit() 함수를 사용하는데, 그 인자에 따라 학습 과정 및 결과가 차이납니다. 학습과정이 어떤 방식으로 일어나는 지 살펴보도록 하겠습니다.

배치사이즈와 에포크

케라스에서 만든 모델을 학습할 때는 fit()함수를 사용합니다.

model.fit(x, y, batch_size=32, epochs=10)

주요인자는 다음과 같습니다.

  • x : 입력 데이터
  • y : 라벨 값
  • batch_size : 몇 개의 샘플로 가중치를 갱신할 것인지 지정
  • epochs : 학습 반복 횟수

학습에 관련된 인자이므로 시험 공부하는 것에 비유를 해보겠습니다. 먼저 모의고사 1회분을 가지고 학습해봅시다. 이 1회분은 100문항이 있고, 해답지도 제공합니다. 문제를 푼 뒤 해답지와 맞춰보면서 학습이 이루어지기 때문에 해답지가 없으면 학습이 안 됩니다.

img

위의 주요인자은 다음과 같이 비유할 수 있습니다.

x

100문항의 문제들입니다.

y

100문항의 답들입니다.

batch_size(배치사이즈)

배치사이즈는 몇 문항을 풀고 해답을 맞추는 지를 의미합니다. 100문항일 때, 배치사이즈가 100이면 전체를 다 풀고 난 뒤에 해답을 맞춰보는 것입니다. 우리가 해답을 맞춰볼 때 ‘아하, 이렇게 푸는구나’라고 느끼면서 학습하는 것처럼 모델도 이러한 과정을 통해 가중치가 갱신됩니다.

문제를 푼 뒤 해답과 맞춰봐야 학습이 일어납니다. > 모델의 결과값과 주어진 라벨 값과의 오차를 줄이기 위해, `역전파(Backpropagation)` 알고리즘으로 가중치가 갱신됩니다.

전체 문제를 푼 뒤 해답과 맞추므로 이 때 가중치 갱신은 한 번만 일어납니다.

img

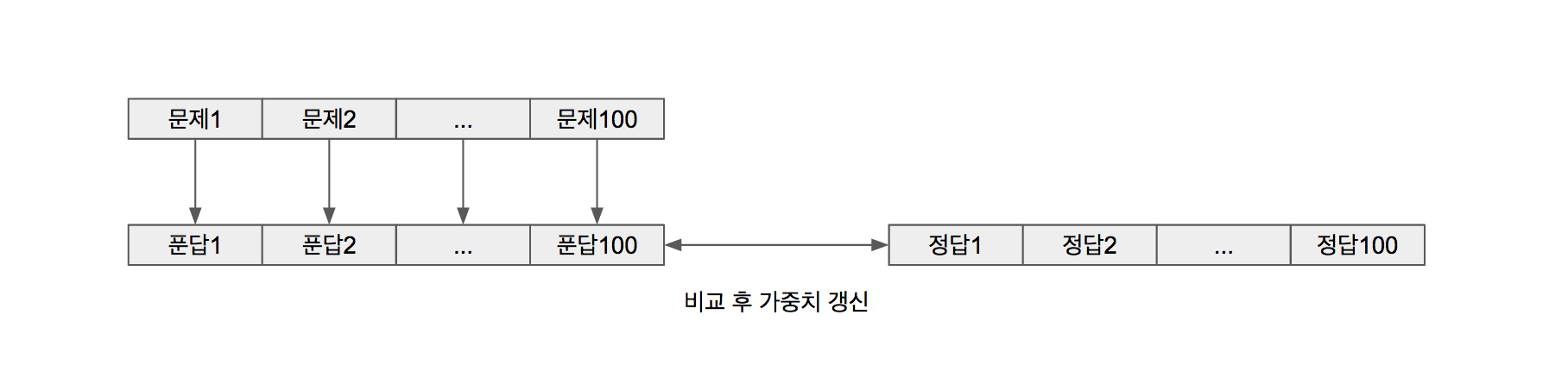
배치사이즈가 10이면 열 문제씩 풀어보고 해답 맞춰보는 것입니다. 100문항을 10문제씩 나누어서 10번 해답을 맞추므로 가중치 갱신은 10번 일어납니다.

img

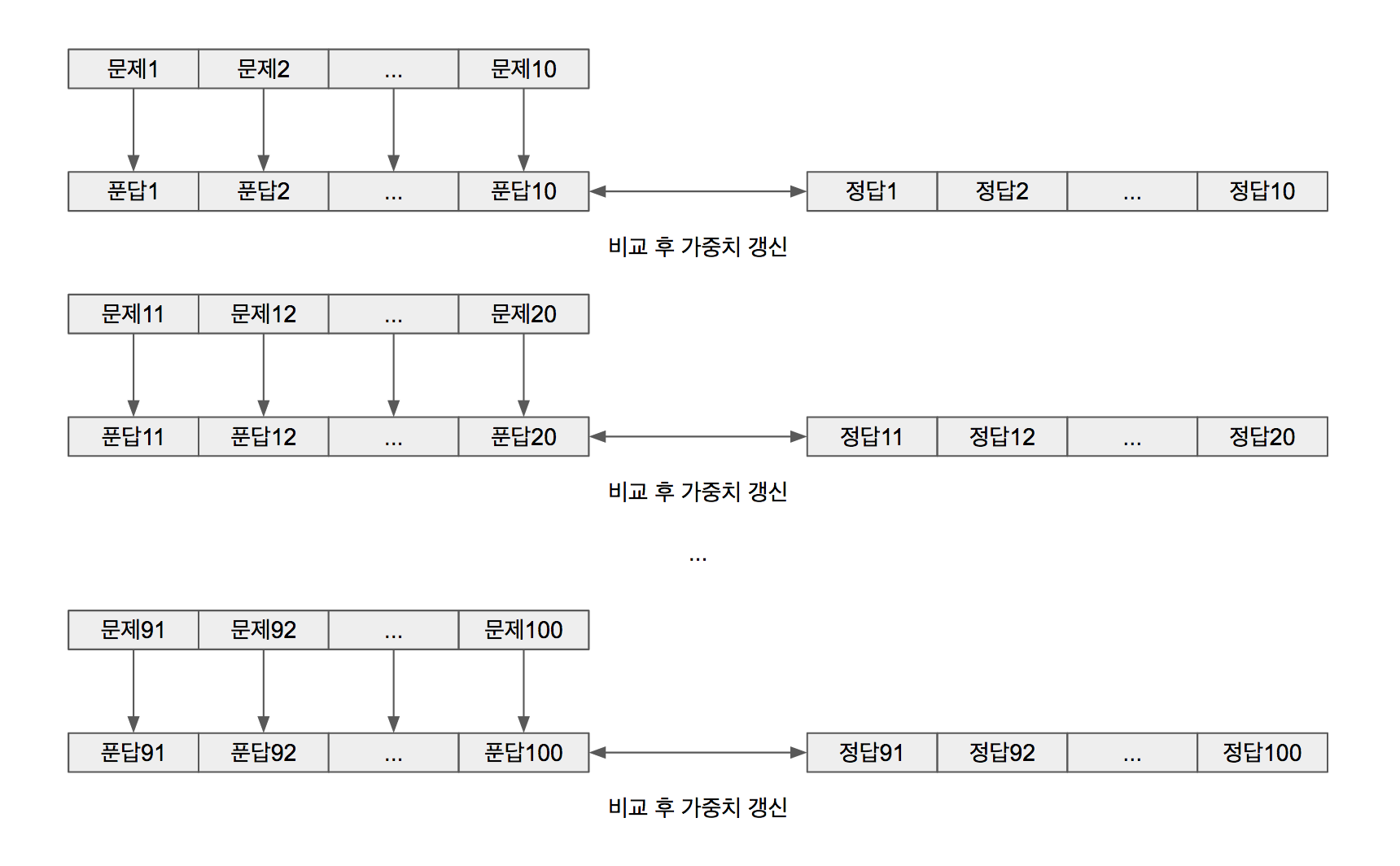
배치사이즈가 1이면 한 문제 풀고 해답 맞춰보고 또 한 문제 풀고 맞춰보고 하는 것입니다. 한 문제를 풀 때마다 가중치 갱신이 일어나므로 횟수는 100번입니다.

img

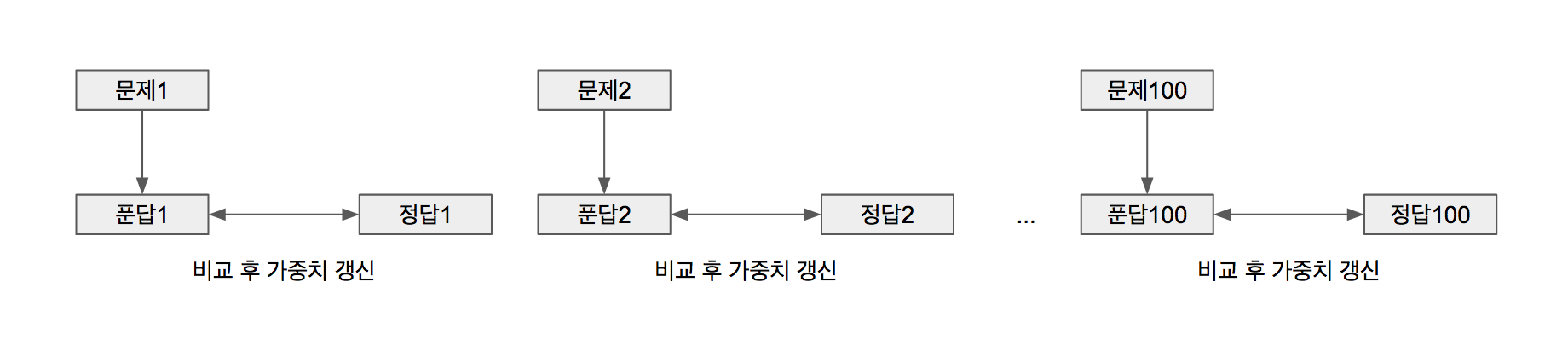
100문제 다 풀고 해답을 맞히는 것과 1문제씩 풀고 해답을 맞히는 것은 어떤 차이가 있을까요? 언뜻 생각해서는 별 반 차이가 없어 보입니다. 하지만 모의고사 1회분에 비슷한 문항이 있다고 가정했을 때, 배치사이즈가 100일 때는 다 풀어보고 해답을 맞춰보기 때문에 한 문제를 틀릴 경우 이후 유사 문제를 모두 틀릴 경우가 많습니다. 배치사이즈가 1인 경우에는 한 문제씩 풀어보고 해답을 맞춰보기 때문에 유사문제 중 첫 문제를 틀렸다고 하더라도 해답을 보면서 학습하게 되므로 나머지 문제는 맞추게 됩니다. 자 그럼 이 배치사이즈가 어떨 때 학습효과가 좋을까요? 사람이 학습하는 것이랑 비슷합니다. 100문항 다 풀고 해답과 맞추어보려면 문제가 무엇이었는지 다 기억을 해야 맞춰보면서 학습이 되겠죠? 기억력(용량)이 커야합니다. 1문항씩 풀고 해답 맞추면 학습은 꼼꼼히 잘 되겠지만 시간이 너무 걸리겠죠? 그리고 해답지를 보다가 다음 문제의 답을 봐버리는 불상사가 생기겠죠(이것은 컴퓨터에서는 일어나지 않는 일입니다).

배치사이즈가 작을수록 가중치 갱신이 자주 일어납니다.

epchos(에포크)

에포크는 모의고사 1회분을 몇 번 풀어볼까 입니다. 즉 100문항의 문제들을 몇 번이나 반복해서 풀어보는 지 정하는 것입니다. 에포크가 20이면 모의고사 1회분을 20번 푸는 것입니다. 처음에는 같은 문제를 반복적으로 풀어보는 것이 무슨 효과가 있는 지 의문이 들었지만 우리가 같은 문제집을 여러 번 풀면서 점차 학습되듯이 모델도 같은 데이터셋으로 반복적으로 가중치를 갱신하면서 모델이 학습됩니다. 같은 문제라도 이전에 풀었을 때랑 지금 풀었을 때랑 학습상태(가중치)가 다르기 때문에 다시 학습이 일어납니다.

같은 문제집이라도 반복해서 풀면 학습이 일어납니다.

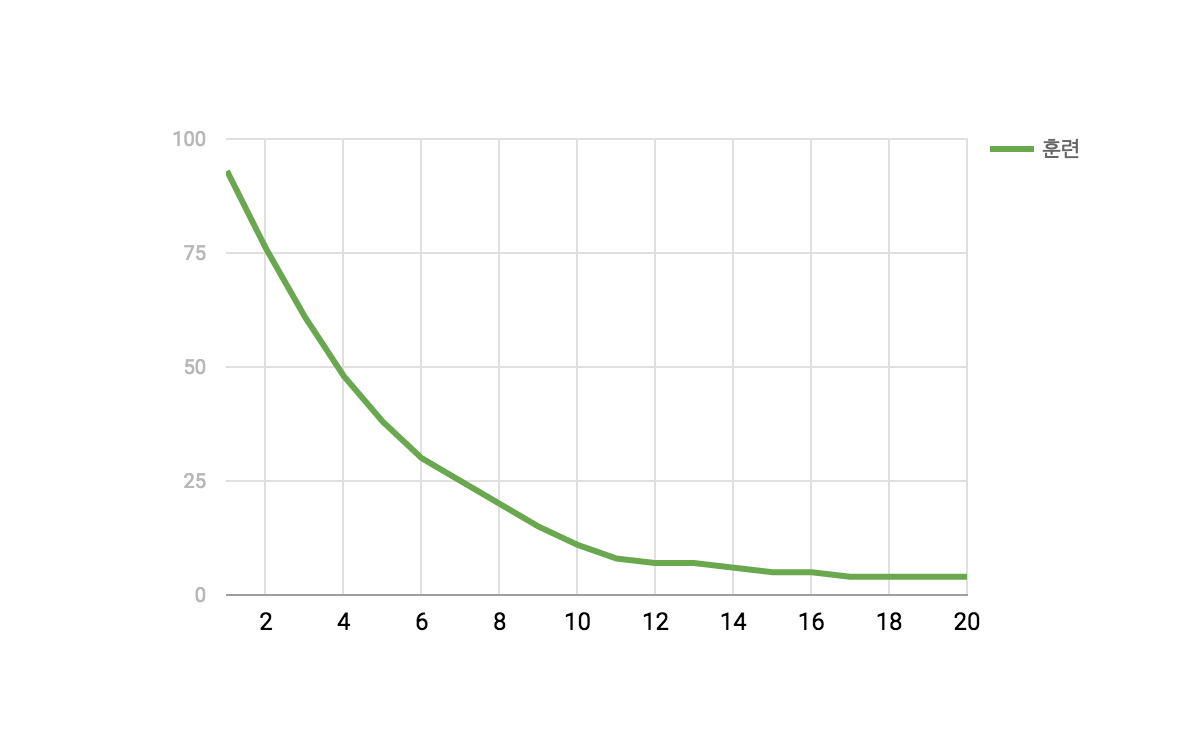
아래 그래프에서 세로축이 100문항 중 틀린 개수이고, 가로축이 모의고사 풀이 반복횟수입니다. 풀이를 반복할수록 틀린 개수가 적어지는 것을 보실 수 있습니다. 처음에는 틀린 개수가 확 적어지만 반복이 늘어날수록 완만하게 틀린 개수가 줄어듭니다. 우리가 공부할 때도 낮은 점수에서는 공부를 조금하면 점수가 확 오르지만, 높은 점수에서 1~2점 올리는 것이 쉽지 않은 것과 비슷할 수 있습니다.

plot

모의고사 1회분을 20번 푸는 것과 서로 다른 모의고사 20회분을 1번 푸는 것과는 어떤 차이가 있을까요? 이것은 분야에 따라 데이터특성에 따라 다를 것이라고 생각합니다. 잡다한 문제를 많이 푸는 것보다 양질의 문제를 여러 번 푸는 것이 도움이 된다고 생각합니다. 피아노를 배울 때도 기본 곡을 반복적으로 학습하면 다양한 악보도 쉽게 보는 반면 이곡 저곡 연습하면 제대로 익히기 쉽지 않습니다. 이런 문제를 제외하고도 현실적으로 데이터를 구하기가 쉽지 않기 때문에 제한된 데이터셋으로 반복적으로 학습하는 것이 효율적입니다.

Q & A

Q1) 그럼 에포크를 무조건 늘리면 좋은가요?

A1) 아닙니다. 하나의 문제집만 계속 학습하면 오히려 역효과가 발생할 수 있습니다. 피아노 칠 때 처음에 곡을 연습할 때는 악보를 보면서 치다가 다음엔 악보안보고도 치고, 나중엔 눈감고도 칩니다. 눈감고만 치다보면 악보 보는 법을 까먹게 되고 다른 곡을 치지 못하는 지경에 이릅니다. 연습한 곡은 완벽하게 칠 지 몰라도 다른 곡은 치지 못하는 상태가 됩니다. 우린 이것을 오버피팅(overfitting)이라고 부릅니다. 악보보고 잘 치는 정도에서 그만 연습하는 것이 더 좋았을 수 있습니다. 실제로 모델을 학습할 때도 오버피팅이 일어나는 지 체크하다가 조짐이 보이면 학습을 중단합니다.

과유불급

요약

딥러닝 모델을 처음 접할 때 어떻게 학습되는 지 이해하기가 쉽지 않습니다. 하지만 공부하면 할수록 사람이 학습하는 방식과 크게 다를 바가 없다는 것이 느껴집니다. 공부를 잘하는 방법에 대해서 연구를 많이 하는 것 처럼 딥러닝 분야에서도 어떻게 학습하는 지에 대해서 연구가 많이 되고 있습니다.

같이 보기