안녕? 레고사람, 안녕? 딥러닝 모델

딥러닝 모델을 레고사람으로 비유해보고 어떻게 모델을 사용하고 학습하는 지 살펴보도록 하겠습니다.

레고 사람과 딥러닝 모델

여기에 레고사람 하나와 딥러닝 모델 하나가 있습니다. 이 둘을 매칭해보겠습니다.

레고 사람은 크게 머리, 상반신, 하반신 이렇게 3가지로 나눌 수 있습니다. 각각 특징을 살펴보겠습니다.

• 머리 : 눈과 입이 있고, 보이지는 않지만 생각할 수 있는 뇌가 있습니다.
• 상반신 : 몸통과 두 팔이 달려있고, 두 손은 무언가를 잡을 수가 있습니다.

• 하반신 : 두 다리가 있으며 걸을 수 있습니다.

  레고 사람은 머리, 상반신, 하반신으로 구성되어 있다.

이번에는 딥러닝 모델을 살펴보겠습니다. 딥러닝 모델은 크게 네트워크, 목표함수, 최적화기로 구성되어 있습니다.

• 네트워크 : 여러층의 다양한 레이어로 구성되어 있습니다. 이렇게 쌓은 레이어에 데이터를 입력하면, 레이어들의 내부 연산을 통해 결과값이 출력됩니다.
• 목표함수 : 딥러닝 모델의 학습 목표를 설정하는 것이며, 학습 목표 기준으로 네트워크의 출력과 실제 정답이 얼마나 차이나는 지를 계산합니다.

• 최적화기 : 목표함수로부터 계산된 차이에 따라 네트워크를 갱신합니다.

  딥러닝 모델은 네트워크, 목표함수, 최적화기로 구성되어 있다.

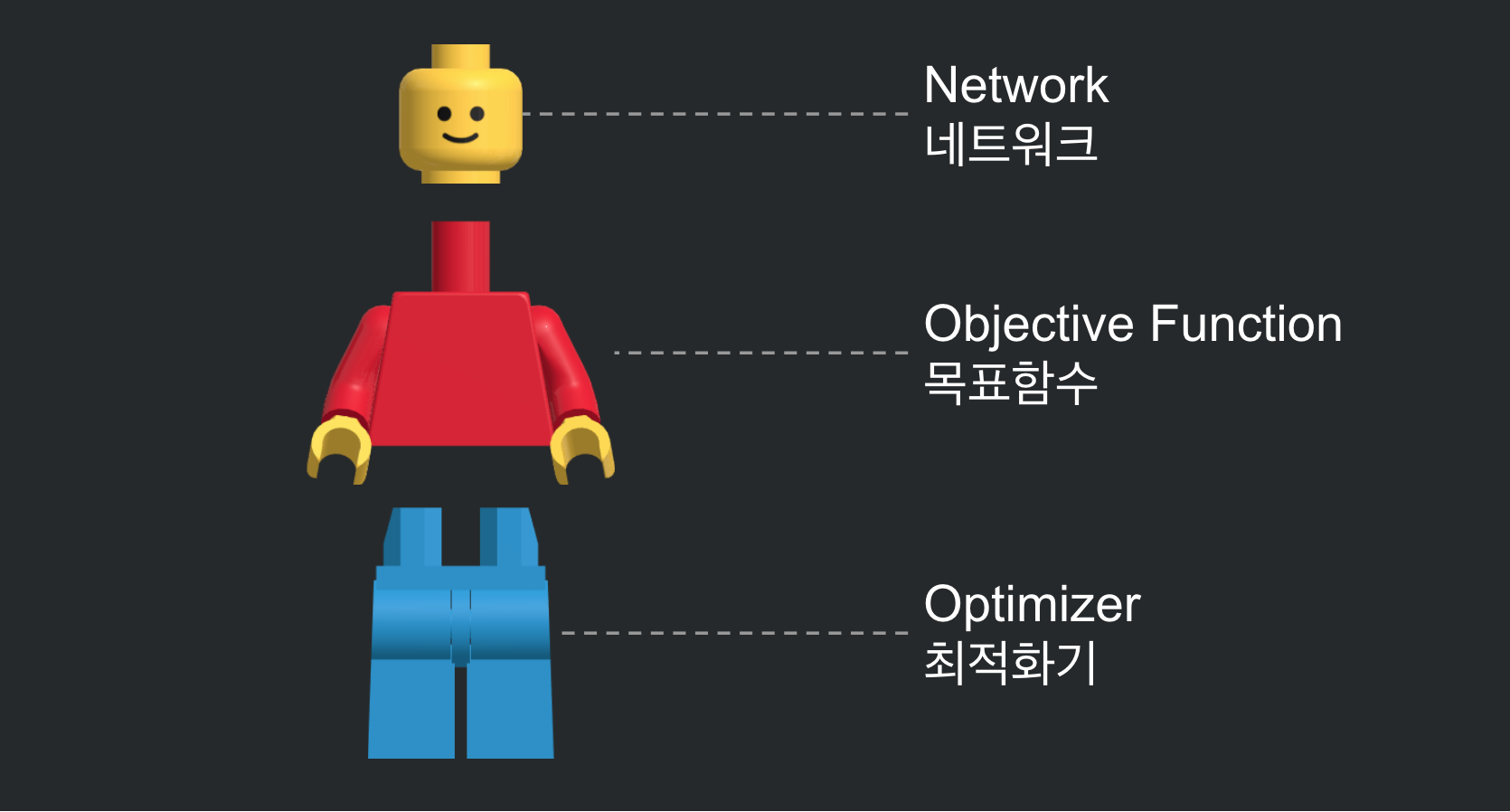
레고 사람과 딥러닝 모델을 매칭하면 다음과 같습니다.

• 머리 = 네트워크
• 상반신 = 목표함수
• 하반신 = 최적화기

레고 사람 머리 이용하기

레고 사람의 머리를 좀 더 살펴보겠습니다. 머리를 보면, 눈, 입이 있고, 보이지 않지만 뇌가 있다고 가정을 해보겠습니다. 이 뇌가 딥러닝 모델에서의 네트워크를 말하며, 네트워크는 다시 아키텍처와 가중치로 구성됩니다. 아키텍처는 구성된 레이어들의 내부 및 연결 구조를 말하며, 각 레이어들 속에 입력 뉴런과 출력 뉴런과의 연결강도를 의미하는 가중치 정보가 포함되어 있습니다. 레이어를 레고 블록으로 표시할 수 있으며, 몇 개의 블록을 조립하여 아키텍처를 구성할 수 있습니다. 즉 머리 안에는 조립된 레고 블록이 들어가 있다고 생각하시면 됩니다. 레고 블록에 대해서 더 궁금하시면 ‘블록과 함께하는 파이썬 딥러닝 케라스’ 책을 참고하세요.

정보가 눈으로 들어가면 이 정보가 네트워크에 입력입니다. 입력된 정보는 네트워크의 아키텍처와 가중치에 의해 결과값이 계산되고 이 값이 입으로 출력됩니다. 이 과정을 다음 그림처럼 나타낼 수 있습니다.

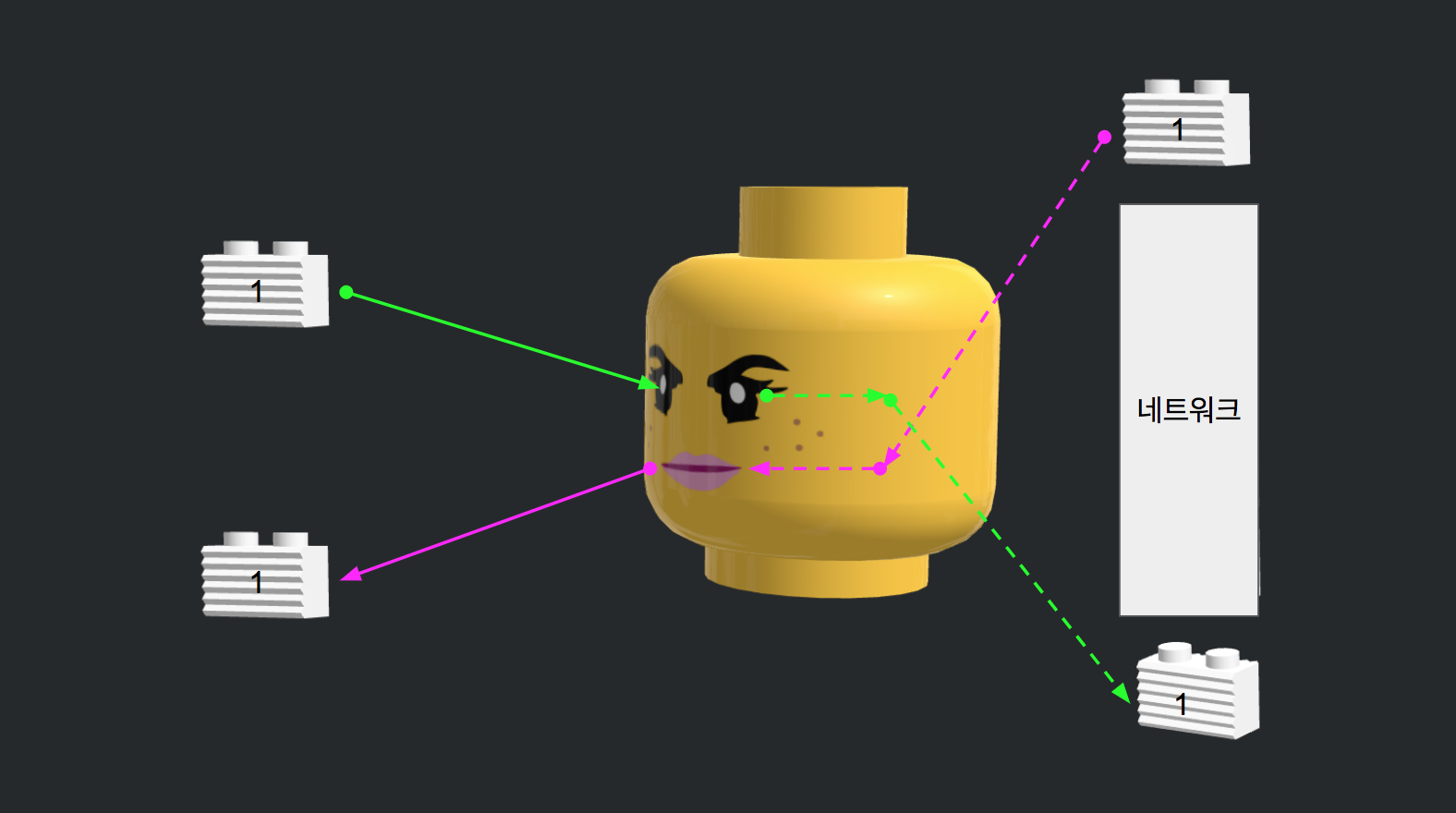
우리가 딥러닝 모델에 원하는 작동은 입력이 주어졌을 때, 출력이 나오는 것입니다. 이를 위해서는 레고 사람 머리 즉 네트워크만 있어도 딥러닝 모델을 사용할 수 있습니다. 대신 네트워크가 학습이 되지 않은 상태이기 때문에 랜덤한 출력이 나오겠죠? 정말 네트워크만으로 작동이 가능한 지 케라스 코드로 확인해보겠습니다. 먼저 문제 정의를 해야겠죠? 가장 쉬운 개념인 ‘크다’, ‘작다’부터 풀어볼까요? 1에서 5까지 숫자 중 하나를 불러주면 ‘작다’라고 대답하고, 6에서 10까지 숫자 중 하나를 불러주면 ‘크다’라고 대답하는 문제입니다.

먼저 딥러닝 모델을 하나 만들어봅니다.

model = Sequential()

모델은 만들긴 했지만 아무것도 없는 비어있는 모델입니다. 문법을 조금 살펴보면 “A = B”라는 코드는 “B의 결과를 A에 대입한다”라는 의미입니다. 여기서는 “Sequential()”은 모델을 생성한 뒤 그 모델은 반환하는 데 그 반환값을 “model”에 저장한다는 정도로 해두죠. 여기서 “반환”이란 의미는 “결과” 또는 “출력”정도로 이해하시면 됩니다. 이제 “model”이라는 모델이 생겼으니 여기에 네트워크를 심어보도록 하죠.

model.add(Dense(64, input_dim=1, activation='relu')) # 입력이 숫자 하나이고 출력이 64개인 레이어입니다.
model.add(Dense(64, activation='relu')) # 입력이 64개이고, 출력이 64개인 레이어입니다.
model.add(Dense(64, activation='relu')) # 입력이 64개이고, 출력이 64개인 레이어입니다.
model.add(Dense(64, activation='relu')) # 입력이 64개이고, 출력이 64개인 레이어입니다.
model.add(Dense(1, activation='sigmoid')) # 입력이 64개이고 출력이 1개인 레이어입니다.

model에는 “add”라는 함수를 가지고 있는데, 이 함수를 이용해서 레이어를 추가할 수 있습니다. 레이어를 추가한다는 의미는 모델의 네트워크에 추가한다는 것이며 네트워크의 아키텍처를 정의하는 것입니다. 즉 사람에 비유하자면 뇌의 구조를 정의한다는 것과 비슷하다고 보시면 됩니다. 여기서는 “Dense”라는 레이어로 “add”를 다섯 번 호출했으니, 현재 네트워크의 레이어가 다섯층으로 구성되었음을 알 수 있습니다. “Dense” 레이어의 상세 내용은 나중에 살펴보기로 하고, 지금은 첫번째 인자의 숫자와 input_dim에 대해서만 설명드리겠습니다. 첫번째 인자는 출력 뉴런의 수를 의미하고 input_dim은 입력 뉴런의 수를 의미힙니다. 위의 코드를 글로 적어오면 다음과 같습니다.

• 첫번째 레이어는 하나를 입력해서 64개를 출력한다.
• 두번째 레이어는 64개를 입력해서 64개를 출력한다. 코드에서는 64개 입력에 대한 명시적으로 표시는 되어 있지 않지만 첫번째 레이어의 출력을 입력으로 삼기 때문에 64개이다.
• 세번째 레이어는 64개를 입력해서 64개를 출력한다. 코드에서는 64개 입력에 대한 명시적으로 표시는 되어 있지 않지만 두번째 레이어의 출력을 입력으로 삼기 때문에 64개이다.
• 네번째 레이어는 64개를 입력해서 64개를 출력한다. 코드에서는 64개 입력에 대한 명시적으로 표시는 되어 있지 않지만 세번째 레이어의 출력을 입력으로 삼기 때문에 64개이다.
• 다섯번째 레이어는 64개를 입력해서 1개를 출력한다. 코드에서는 64개 입력에 대한 명시적으로 표시는 되어 있지 않지만 네번째 레이어의 출력을 입력으로 삼기 때문에 8개이다.

그리고 activation이라는 옵션이 보이죠? 이것은 출력을 어떻게 변화할 것인가를 나타내는 것입니다. 여기서는 마지막 레이어에서 사용된 ‘시그모이드(sigmoid)’만 설명을 먼저하도록 하겠습니다. 시그모이드는 출력 뉴런의 결과값을 0.0과 1.0사이의 값으로 출력되도록 변환합니다. 어떠한 값이 출력 뉴런에 있던 간에 0.0과 1.0 사이의 값으로 바꿔서 출력이 되겠죠? 이러한 특성 때문에 이진 분류하는 문제에 주로 사용됩니다. 0.5를 기준으로 크면 ‘양성’, 작으면 ‘음성’으로 결정하기 편하기 때문이죠. 지금 우리가 풀려고 하는 문제도 “크다”와 “작다”를 분류하기 위한 이진분류 문제이므로 시그모이드를 사용하겠습니다. 지금까지 코드를 정리해보면 다음과 같습니다.

• 빈 모델하나 만듬
• 만든 모델에 세 개의 레이어를 추가해서 네트워크를 구성함
• 이 네트워크는 최초 입력이 하나고 최종 출력도 하나임
• 최종 출력은 0.0과 1.0 사이의 값이 나오도록 설정됨

우리가 이 모델에서 원하는 결과는 무엇일까요? 0이라고 출력하면 작다라는 의미이고, 1이라고 출력하면 크다라는 의미라고 했을 때, 1에서 5까지 숫자를 입력하면, 0으로 출력하고, 6에서 10까지 숫자를 입력하면 1으로 출력하길 원합니다. 그럼 우리가 만든 네트워크에 숫자 3을 입력해보겠습니다. 우리가 원하는 값은 1과 5사이의 숫자이니 0이라고 출력되면 좋겠죠?

X_hat = np.array([[3]]) # numpy 패키지를 이용해서 숫자 '3'인 입력을 하나 만듭니다.
Y_hat = model.predict(X_hat) # 앞서 만든 숫자 '3'을 모델의 네트워크에 입력한 뒤 계산된 출력값을 Y_hat에 저장합니다.
print(Y_hat) # y_hat을 화면에 출력합니다.

조금 복잡한 코드가 나왔지만 이를 간단히 설명하면 다음과 같습니다.

• 숫자 3을 X_hat이라고 하고,
• 이 X_hat을 model에 입력하여 예측해봐(predict)라고 했을 때 나온 출력을 Y_hat에 저장한 후
• 이 Y_hat을 화면에 출력함

그럼 전체 소스코드를 실행해보겠습니다. 앞부분은 필요한 패키지를 불러오는 것인데 Sequential()이나 Dense() 그리고 np 등 함수 및 모듈을 사용하기 위해 필요한 설명서를 읽어드린다고 생각하시면 됩니다.

# 필요한 패키지를 불러옵니다.
from keras.models import Sequential
from keras.layers import Dense
import numpy as np

# 시퀀스 모델을 생성합니다.
model = Sequential()

# 생성한 시퀀스 모델에 5개 레이어를 쌓습니다. 
model.add(Dense(64, input_dim=1, activation='relu')) # 입력이 숫자 하나이고 출력이 64개인 레이어입니다.
model.add(Dense(64, activation='relu')) # 입력이 64개이고, 출력이 64개인 레이어입니다.
model.add(Dense(64, activation='relu')) # 입력이 64개이고, 출력이 64개인 레이어입니다.
model.add(Dense(64, activation='relu')) # 입력이 64개이고, 출력이 64개인 레이어입니다.
model.add(Dense(1, activation='sigmoid')) # 입력이 64개이고 출력이 1개인 레이어입니다.

X_hat = np.array([[3]]) # numpy 패키지를 이용해서 숫자 '3'인 입력을 하나 만듭니다.
Y_hat = model.predict(X_hat) # 앞서 만든 숫자 '3'을 모델의 네트워크에 입력한 뒤 계산된 출력값을 Y_hat에 저장합니다.

print(Y_hat) # y_hat을 화면에 출력합니다.

[[ 0.78475791]]

Using TensorFlow backend.

제 경우 0.78이 나왔네요. 숫자 3은 1과 5사이의 숫자이니 0에 가까운 수가 나와야 되는데 말이죠. 우리가 네트워크를 정의하긴 했지만 현재 아무런 데이터도 학습을 하지 않은 상태이기 때문에 숫자 3이 네트워크에 입력되었을 경우 랜덤으로 설정된 네트워크의 가중치로 계산되어 출력값도 랜덤값이 나온 것입니다. 다만 출력층의 activation 함수가 시그모이드(sigmoid)라서 0.0과 1.0값 사이로 나오긴 하지만요.

학습하지 않은 네트워크는 마치 갓 태어난 아기가 옹알이하는 것과 같이 랜덤값을 출력한다.

자 그럼, 우리가 원하는 모델을 만들기 위해 무엇을 해야될까요? 맞습니다. 네트워크를 학습시켜야 합니다. 네트워크를 학습시키기 위해서는 목표함수와 최적화기가 필요하며, 레고 사람 비유에서는 상반신과 하반신이 필요합니다. 딥러닝 모델이 학습된 이후 사용할 때는 역시 네트워크만 있으면 됩니다.

레고 사람 조립하기

자 이제 머리, 상반신, 하반신을 꽂아서 하나의 레고 사람으로 만들어보겠습니다. 이 과정은 네트워크, 목표함수, 최적화기를 하나로 묶어 딥러닝 모델을 만드는 것과 같습니다. 케라스에서는 이 과정을 ‘컴파일’이라고 부릅니다.

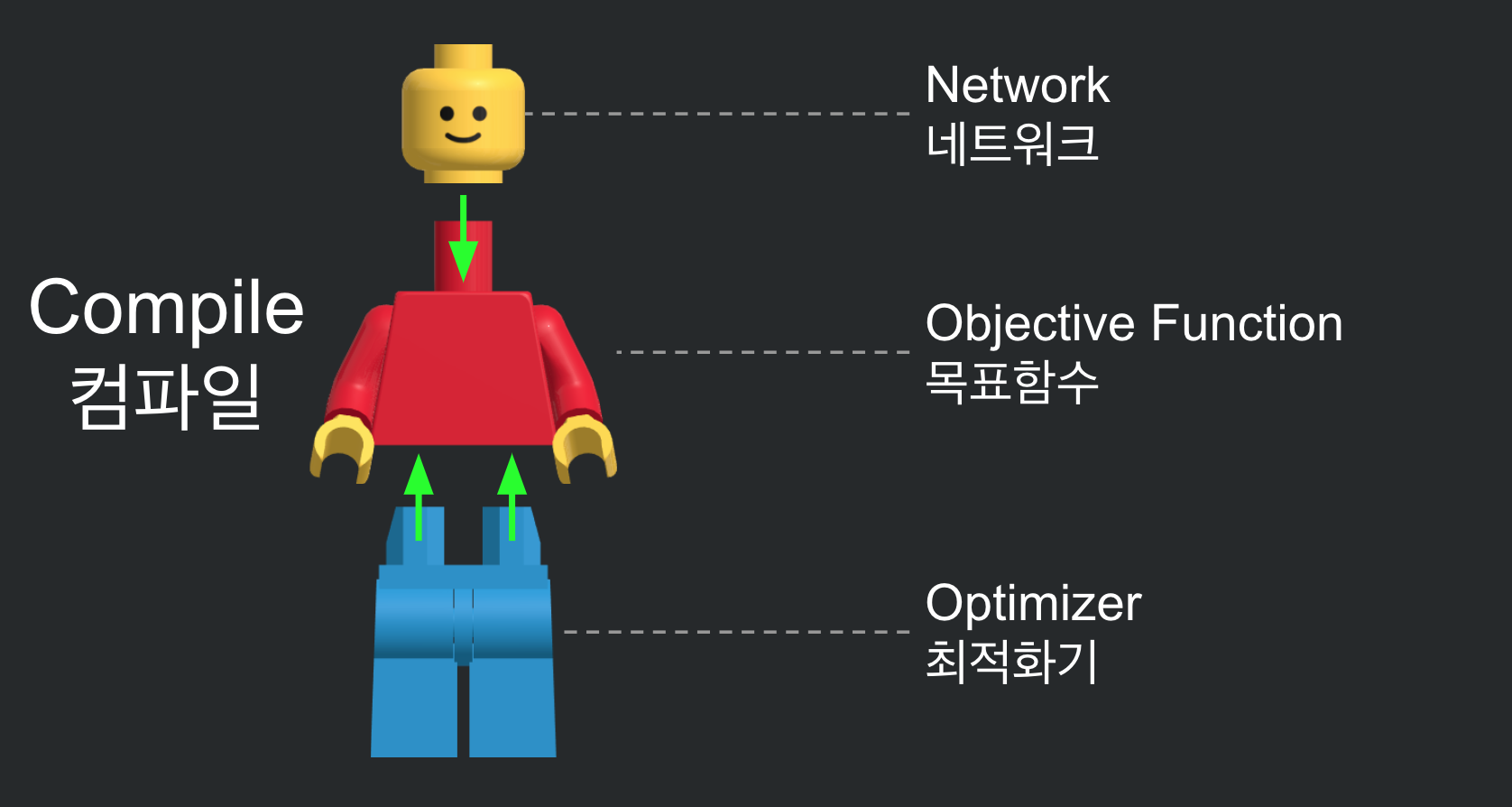
머리, 상반신, 하반신이 하나씩만 있으면 쉽게 조립할 수 있겠지만, 여러개의 레고 사람들이 분리되어 있다면 조립하기가 쉽지가 않습니다. 모두 제 짝이 있기 때문에 잘 맞추어야 제대로된 레고 사람이 나오겠죠? 즉 우리는 어떤 문제를 풀기 위해 적절한 네트워크, 목표함수, 최적화기를 골라 컴파일하여 모델을 구성해야 합니다.

‘크다’와 ‘작다’를 구분하는 문제에서는 두가지를 분류하는 이진분류이므로 목표함수는 ‘binary_crossentropy’으로 설정하고, 최적화기는 일반적으로 사용되는 ‘adam’으로 설정해보겠습니다. 이를 레고 사람으로 표시하면 다음과 같습니다.

위 레고 사람을 케라스 코드로 표현하면 다음과 같습니다. complie 함수에 loss 인자에는 목표함수를 설정하고, optimizer 인자에는 최적화기를 설정합니다.

model.compile(loss='binary_crossentropy', optimizer='adam')

컴파일까지 하였다면 모델이 학습할 준비를 마치게 된 것입니다. 그럼 학습을 시켜볼까요?

레고 사람 학습시키기

학습 과정 이해하기 위해 먼저 아래 간단한 수식을 살펴보겠습니다. 앞에서 네트워크의 출력은 아키텍처와 가중치에 의해 계산된다고 설명드렸는데, 바로 이 간단한 수식으로 계산이 되는 것입니다.

Y' = w * X + b

각 변수의 의미는 다음과 같습니다.

Y' : 네트워크에 의해 계산된 결과값 (푼답)
w, b : 네트워크의 가중치
X : 네트워크의 입력값 (문제)

이것은 마치 학생이 문제를 푸는 것과 동일합니다. 하지만 학생이 제대로 풀었는 지 확인하기 위해서는 정답도 있어야 겠죠? 이 정답을 Y이라고 하죠. 정답을 학생한테 알려주면 푼답(Y’)과 정답(Y)을 비교한 후 ‘아하’라고 하면서 학습을 하게 됩니다. 즉 머리 속의 가중치(w, b)가 갱신되는 것입니다. 그래서 학습을 위해 우리가 준비해야할 것은 바로 문제(X)와 정답(Y)입니다.

우리가 준비해야 할 것은 문제(X)와 정답(Y)이다.

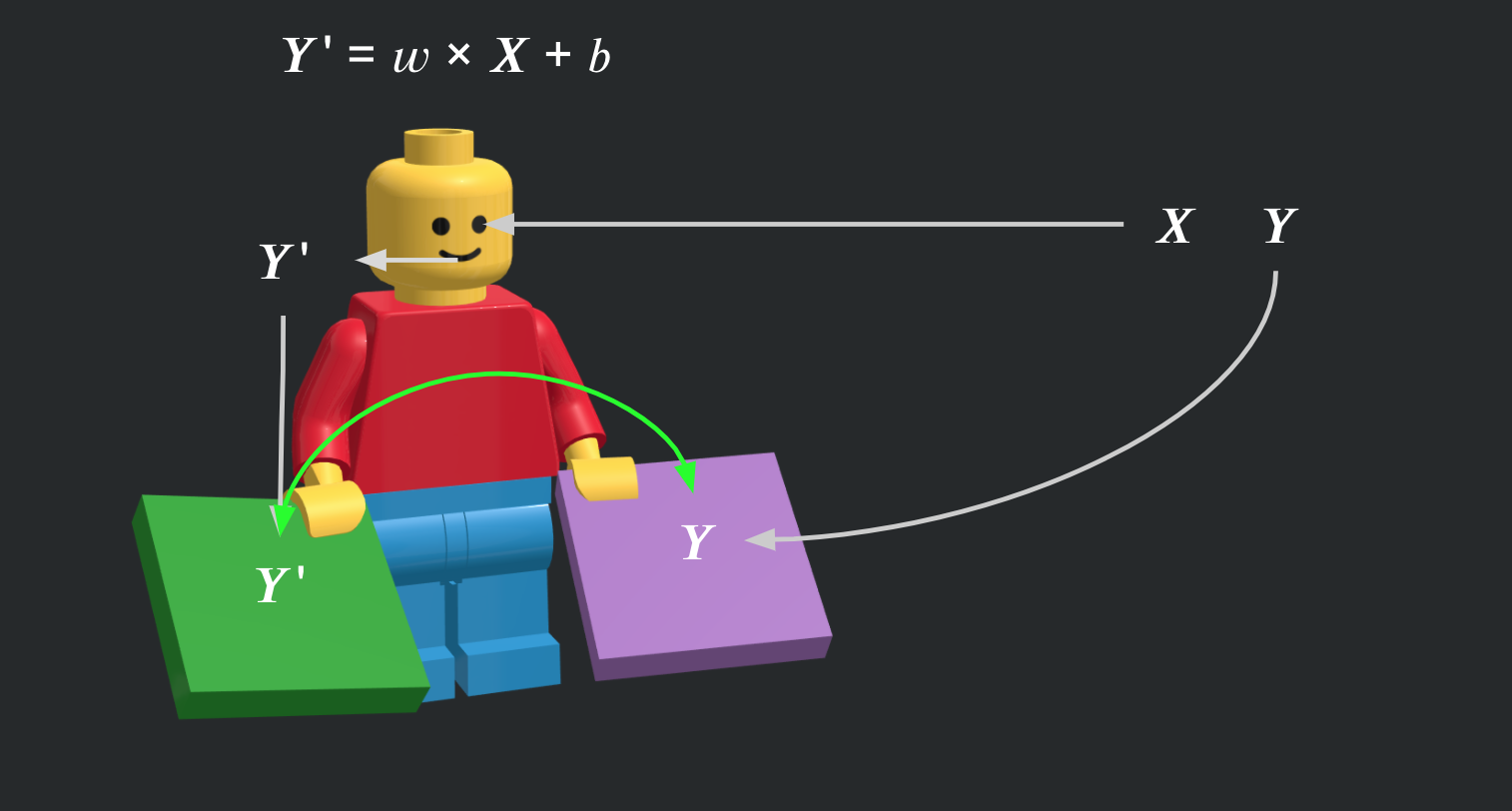
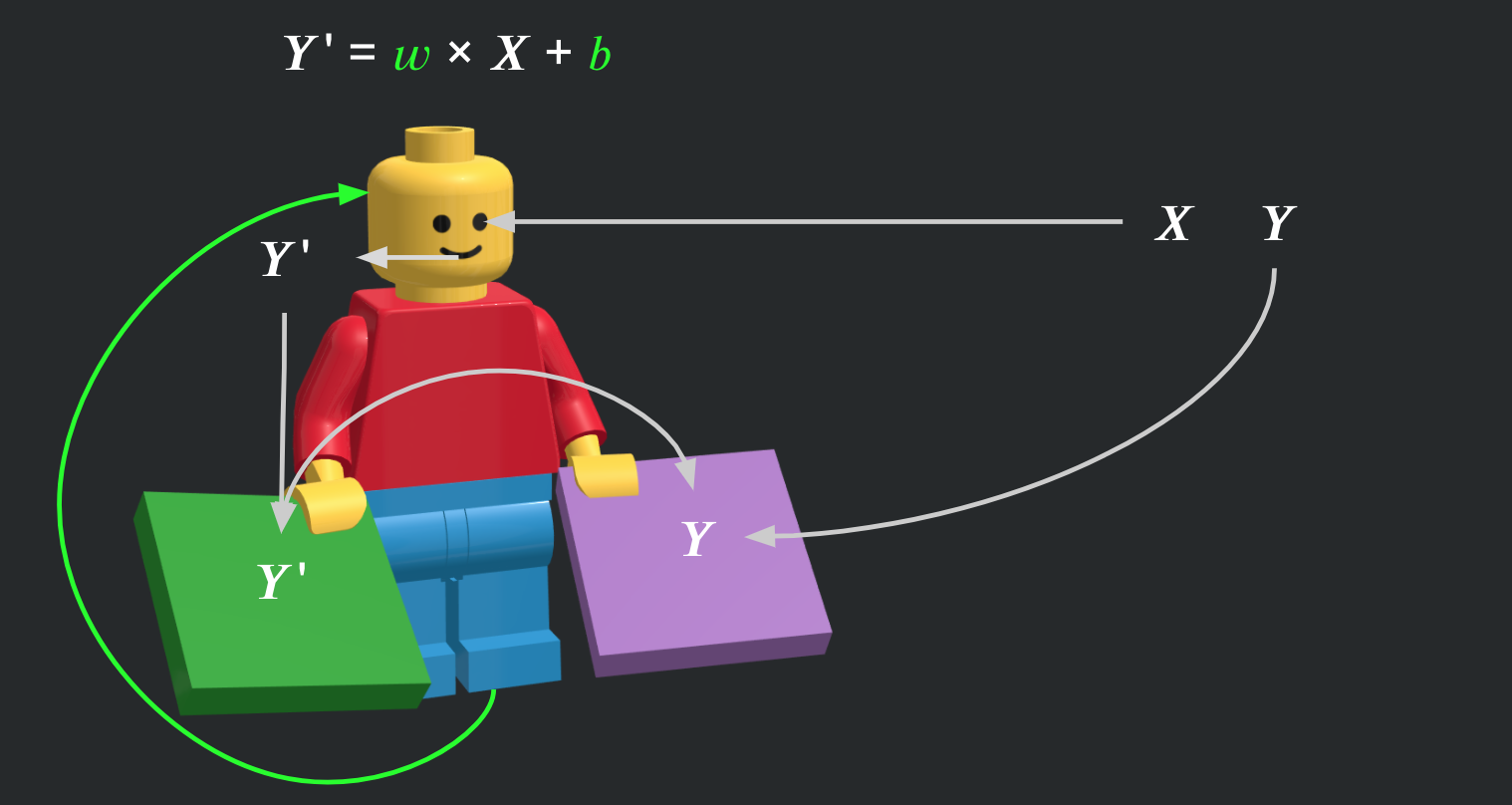
그럼 본격적으로 레고 사람을 학습시켜보겠습니다. 아래 그림처럼 앞서 조립한 레고 사람과 우리가 준비한 X, Y가 있다고 가정해봅니다.

우리가 준비한 X(문제)를 레고 사람의 네트워크에 입력하면, 네트워크는 현재 가지고 있는 가중치(w, b)를 이용하여 Y’ = w * X + b 식에 의해 Y’(푼답)을 출력합니다.

그 다음 상반신(목표 함수)의 한 손에는 네트워크가 푼 답인 Y’을 주고, 또 다른 한 손에는 우리가 준비한 정답 Y를 줍니다.

그럼 목표함수는 양 손에 쥔 두 답 Y와 Y’을 비교하여 손실값을 계산합니다. 차이값이 아니라 손실값이라고 말하는 이유는 Y와 Y’이 수치적으로 차이가 많이 나더라도 목표에 따라 손실이 적을 수도 있고 반대로 수치적으로는 차이가 적더라도 손실값이 클 수가 있습니다. 목표함수에서 중요한 것은 푼 답과 정답 사이의 수치적인 차이가 아니라 목표를 달성하기 위해서 얼마나 손실이 일어났는 지를 아는 것입니다.

목표함수로부터 계산한 손실값은 최적화기에 전달됩니다. 최적화기는 정해진 알고리즘에 의해 손실값에 따라 네트워크를 갱신합니다. 엄밀히 얘기하면 네트워크의 가중치가 갱신됩니다. Y’ = w * X + b 식에서 보면 w와 b가 바뀌게 됩니다. 이 과정이 반복되면서 손실값이 작은 방향으로 다시말해 네트워크가 푼 답과 정답과의 차이가 적어지도록 학습됩니다.

학습과정에 대해서 알아봤으니 케라스로 ‘크다’, ‘작다’를 구분하는 모델을 학습시켜보겠습니다. 먼저 학습시켜야 할 문제와 정답을 준비해야겠죠? 아래 코드는 1에서 10까지 숫자들을 X 변수에 넣고, 각 숫자에 해당하는 정답을 Y 변수에 넣습니다. 이 때 1~5사이의 값은 0으로, 6~10사이의 값은 1로 설정합니다.

X = np.array([[1], [2], [3], [4], [5], [6], [7], [8], [9], [10]]) # 숫자 1에서 10까지의 문제 준비
Y = np.array([[0], [0], [0], [0], [0], [1], [1], [1], [1], [1]]) # 숫자 1에서 10까지의 정답 준비, 1~5는 0, 6~10은 1

X, Y를 준비했으니 모델에 학습을 시켜봅니다. 케라스에서는 우리가 준비한 X, Y을 fit 함수에 입력하여 모델을 학습시킵니다. fit 함수의 주요인자로는 에포크와 배치사이즈가 있습니다. 에포크는 우리가 준비한 문제와 정답을 몇 번 반복해서 학습하느냐를 나타내고, 배치사이즈는 몇 문항을 풀고 푼 답과 정답을 맞춰볼까를 지정하는 옵션입니다. 에포크가 100이고, 배치사이즈가 5이라면 우리가 준비한 10문항을 100번 반복해서 풀며, 10문항 푼 뒤 푼 답과 정답을 맞추게 됩니다. 결론적으론 총 1000 문항(10문항 x 100 에포크)을 풀게되며, 100번(1000문항 / 10 배치사이즈)의 네트워크 갱신이 일어납니다.

model.fit(X, Y, epochs=100, batch_size=10)

그럼 학습 과정이 포함된 전체 소스코드를 살펴보겠습니다.

# 필요한 패키지를 불러옵니다.
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
from keras.utils import np_utils

# 시퀀스 모델을 생성합니다.
model = Sequential()

# 생성한 시퀀스 모델에 5개 레이어를 쌓습니다. 
model.add(Dense(64, input_dim=1, activation='relu')) # 입력이 숫자 하나이고 출력이 64개인 레이어입니다.
model.add(Dense(64, activation='relu')) # 입력이 64개이고, 출력이 64개인 레이어입니다.
model.add(Dense(64, activation='relu')) # 입력이 64개이고, 출력이 64개인 레이어입니다.
model.add(Dense(64, activation='relu')) # 입력이 64개이고, 출력이 64개인 레이어입니다.
model.add(Dense(1, activation='sigmoid')) # 입력이 64개이고 출력이 1개인 레이어입니다.

# 모델을 학습시키기 위해 목표함수와 최적화기를 구성합니다.
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

# X, Y를 준비합니다.
X = np.array([[1], [2], [3], [4], [5], [6], [7], [8], [9], [10]]) # 숫자 1에서 10까지의 문제 준비
Y = np.array([[0], [0], [0], [0], [0], [1], [1], [1], [1], [1]]) # 숫자 1에서 10까지의 정답 준비, 1~5는 0, 6~10은 1

# 모델을 X, Y로 학습시킵니다.
model.fit(X, Y, epochs=100, batch_size=10)

X_hat = np.array([[3]]) # numpy 패키지를 이용해서 숫자 '3'인 입력을 하나 만듭니다.
Y_hat = model.predict(X_hat) # 앞서 만든 숫자 '3'을 모델의 네트워크에 입력한 뒤 계산된 출력값을 Y_hat에 저장합니다.

print(Y_hat) # Y_hat을 화면에 출력합니다.

Epoch 1/100
10/10 [==============================] - 1s - loss: 0.7724 - acc: 0.5000
Epoch 2/100
10/10 [==============================] - 0s - loss: 0.7079 - acc: 0.4000
Epoch 3/100
10/10 [==============================] - 0s - loss: 0.6634 - acc: 0.5000
...
Epoch 98/100
10/10 [==============================] - 0s - loss: 0.0729 - acc: 1.0000
Epoch 99/100
10/10 [==============================] - 0s - loss: 0.0697 - acc: 1.0000
Epoch 100/100
10/10 [==============================] - 0s - loss: 0.0666 - acc: 1.0000
[[ 0.00627144]]

학습한 모델에 숫자 3을 입력한 결과, 출력으로 0.006이 나왔습니다. 우리가 원하는 데로 0에 가까운 수치가 나왔네요. 결과값이 0.5보다 작으면 ‘작다’를 의미하고 0.5보다 크면 ‘크다’라는 의미입니다.

요약

이번 장에서는 딥러닝 모델을 레고 사람에 비유해보고 어떻게 사용하는 지, 어떤 과정을 통해 학습하는 지 살펴보왔습니다. 그리고 간단한 케라스 소스코드도 구동해서 결과를 확인했습니다. 다음 장에서는 네트워크, 목표함수, 최적화기에는 어떤 종류가 있고, 이들 조합으로 어떤 모델을 만들 수 있는 지 알아보겠습니다.