딥로또 895회
딥러닝 세미나를 하다보면 (특히 RNN이나 LSTM 등 시계열 예측 모델을 설명하다보면) 로또나 주식에 관해 질문을 많이 하십니다. 이와 관련된 질문에는 나름 원칙이 있거나 시계열적 특성이나 인과관계가 있는 데이터에만 예측이 잘될꺼라도 말씀은 드리긴 하지만 신통치 않은 답변인지 만족하시질 못 합니다. 그래서 먼저 딥러닝으로 로또를 하면 안된다는 것을 몸소 보여드리기 위해 매주 테스트를 해볼 예정입니다. 들어가기에 앞서 몇가지 말씀드리겠습니다.

- 로또 같은 독립시행(매 시행마다 특정 결과가 나올 확률이 변하지 않는 것) 확률을 가지는 것에는 예측 모델이 의미가 없을지 모릅니다. 하지만 제가 테스트할 모델은 종속시행(반대로 이전의 시행 결과가 현재의 확률에 영향을 줌)을 전제로 하므로 전제부터가 잘 못된 것을 알고 있으니 이 점에 대해서 지적하지 말아주세요.
- 예측 모델을 어떻게 개발했던 간에 이미 894회라는 결과가 있으니 검증을 해볼 수는 있습니다. 이 검증 방법에 대해서는 논리적인지 합리적인지 논의해볼 가치가 있다고 봅니다.
- 모델 개발을 위해서 입력 특징 벡터를 어떻게 정의하고, 출력 형태를 어떻게 설계해서 사용할 것인가에 대해서는 로또가 아니더라도 비슷한 문제를 풀고 계시는 분들에게는 도움이 되실 듯 합니다.
- 열심히 공부하시는 분들에게 머리 식히자고 (제 머리도 식힐겸) 실험해본 것이니 너무 심각하게 안 받아주셨으면 합니다.
실습을 해보시려는 분은 구글 코랩(참고: 코랩 시작하기)에서 같이 하시죠.
문제정의
데이터를 모았으니 이제 문제정의 먼저 해보겠습니다. 문제정의에 따라 데이터셋과 모델 구성이 달라지니 신중하게 생각할 부분입니다.
문제정의에 따라 데이터셋과 모델 구성이 달라진다.
갑자기 진지모드라 죄송합니다만 계속 이어가겠습니다. 주제가 “로또”인 것을 제외하고는 나름 딥러닝 입문자에게 도움이 될 부분이 많아서 중간중간에 설명이 포함되어 있습니다.
데이터셋 구성
무려 894회차나 되는 나름 빅데이터를 구성했으니 (일주일에 하나씩 나와도 개수가 몇개 안되네요ㅠㅠ) 이를 모델에 학습시키기 위해 데이터셋을 구성해보학습하기
문제정의에 앞서 전제부터 설명하겠습니다. 두 가지 전제가 있는 데요.
- 첫번째 전제: 제가 실험할 모델의 전제는 “로또 번호는 과거부터 미래까지 이미 정해져 있다” 입니다. 즉 지금까지 외운 로또번호를 가지고 과거로 가면 모두 1등이 될 수 있고, 미래에 다녀와서 본 로또 번호를 이번에 제출하면 당첨이 될 수 있다는 것입니다.
- 두번째 전제: 지금까지의 로또번호를 딥러닝에게 외우게 하면 딥러닝이 뭔가 원리를 깨달아서 그 원리대로 그 다음회 로또번호를 예측할 수 있다는 것입니다.
첫번째 전제도 말도 안되지만, 두번째 전제도 더 말도 안됩니다. 두번째 전제인 경우에는 마치 원주율을 어느 소수점짜리까지 학습하면, 그 다음 자리수를 예측한다는 것과 비슷한 얘기입니다. 원주율은 순환하지 않은 무한소수인데요. 원주율이 아래와 같다고 했을 때,
3.14159265358979323846264338327950288419...
아래와 같이 이전 수들로 다음 수를 예측하게 학습시킨 뒤, 마지막 수의 다음을 예측하도록 하는 것입니다.
- 학습과정
- 3 > 1
- 3.1 > 4
- 3.14 > 1
- 3.141 > 5
- …
- 3.141592653589793238462643383279502884 > 1
- 추론과정
- 3.1415926535897932384626433832795028841 > 9(희망)
이게 될리가… 물론 로또가 아닌 규칙이 있는 시계열 데이터인 경우에는 해볼만한 모델이라고 생각합니다.
데이터 수집
전제에서 보면, 결국 과거의 로또 번호로 미래의 번호를 예측하는 것이기에 과거의 로또 번호를 수집해야 합니다. 동행복권 웹페이지에서 당첨된 번호를 알 수 있는데요, 일일이 기록하기가 쉽지 않으니 파이썬 프로그램을 간단히 짜서 자동으로 수집하겠습니다. 이를 “웹 크롤링”이라고 부르더군요. 이 과정이 귀찮으신 분을 위해 일단 894회까지 수집한 데이터는 다운로드 받을 수 있게 링크를 걸어두었습니다.
웹 크롤링 코드는 아래와 같습니다. 웹 크롤링을 하기 전에는 저작권이나 크롤링이 금지된 사이트를 확인해봐야하는 데요, 이러한 정보는 사이트의 “robots.txt”에서 확인해볼 수 있다고 합니다. 다행히 우리가 가져올 동행복권 웹페이지에서는 “robots.txt” 파일이 확인되지 않네요.
웹 크롤링 소스코드는 아래 출처를 기반으로 제작되었고, 상금 등의 부가 정보 수집을 위해서 수정되었습니다.
- 출처: http://cfile25.uf.tistory.com/attach/2529683E5775234E2DF36E
import pandas as pd
import requests
from bs4 import BeautifulSoup
main_url = "https://www.dhlottery.co.kr/gameResult.do?method=byWin" # 마지막 회차를 얻기 위한 주소
basic_url = "https://www.dhlottery.co.kr/gameResult.do?method=byWin&drwNo=" # 임의의 회차를 얻기 위한 주소
# 마지막 회차 정보를 가져옴
def GetLast():
resp = requests.get(main_url)
soup = BeautifulSoup(resp.text, "lxml")
result = str(soup.find("meta", {"id" : "desc", "name" : "description"})['content'])
s_idx = result.find(" ")
e_idx = result.find("회")
return int(result[s_idx + 1 : e_idx])
# 지정된 파일에 지정된 범위의 회차 정보를 기록함
def Crawler(s_count, e_count, fp):
for i in range(s_count , e_count + 1):
crawler_url = basic_url + str(i)
resp = requests.get(crawler_url)
soup = BeautifulSoup(resp.text, "html.parser")
text = soup.text
s_idx = text.find(" 당첨결과")
s_idx = text.find("당첨번호", s_idx) + 4
e_idx = text.find("보너스", s_idx)
numbers = text[s_idx:e_idx].strip().split()
s_idx = e_idx + 3
e_idx = s_idx + 3
bonus = text[s_idx:e_idx].strip()
s_idx = text.find("1등", e_idx) + 2
e_idx = text.find("원", s_idx) + 1
e_idx = text.find("원", e_idx)
money1 = text[s_idx:e_idx].strip().replace(',','').split()[2]
s_idx = text.find("2등", e_idx) + 2
e_idx = text.find("원", s_idx) + 1
e_idx = text.find("원", e_idx)
money2 = text[s_idx:e_idx].strip().replace(',','').split()[2]
s_idx = text.find("3등", e_idx) + 2
e_idx = text.find("원", s_idx) + 1
e_idx = text.find("원", e_idx)
money3 = text[s_idx:e_idx].strip().replace(',','').split()[2]
s_idx = text.find("4등", e_idx) + 2
e_idx = text.find("원", s_idx) + 1
e_idx = text.find("원", e_idx)
money4 = text[s_idx:e_idx].strip().replace(',','').split()[2]
s_idx = text.find("5등", e_idx) + 2
e_idx = text.find("원", s_idx) + 1
e_idx = text.find("원", e_idx)
money5 = text[s_idx:e_idx].strip().replace(',','').split()[2]
line = str(i) + ',' + numbers[0] + ',' + numbers[1] + ',' + numbers[2] + ',' + numbers[3] + ',' + numbers[4] + ',' + numbers[5] + ',' + bonus + ',' + money1 + ',' + money2 + ',' + money3 + ',' + money4 + ',' + money5
print(line)
line += '\n'
fp.write(line)
last = GetLast() # 마지막 회차를 가져옴
fp = open('2020-1-25-keras_lstm_lotto_v895_data.csv', 'w')
Crawler(1, last, fp) # 처음부터 마지막 회차까지 저장
fp.close()
번호를 기록한 파일을 열어보면 아래와 같이 각 회차마다 한 행으로 되어 있고, 각 열은 쉼표로 구분되어 있습니다.
1,10,23,29,33,37,40,16,0,143934100,5140500,113400,10000
2,9,13,21,25,32,42,2,2002006800,94866800,1842000,100800,10000
3,11,16,19,21,27,31,30,2000000000,0,1174100,54900,10000
4,14,27,30,31,40,42,2,0,211191200,7282400,152100,10000
5,16,24,29,40,41,42,3,0,0,6033800,166500,10000
...
894,19,32,37,40,41,43,45,2377935959,63694714,1530204,50000,5000
각 열의 의미는 다음과 같습니다.
- 회차
- 첫번째 당첨번호
- 두번째 당첨번호
- 세번째 당첨번호
- 네번째 당첨번호
- 다섯번째 당첨번호
- 여섯번째 당첨번호
- 보너스 번호
- 1등 당첨금액
- 2등 당첨금액
- 3등 당첨금액
- 4등 당첨금액
- 5등 당첨금액
문제정의
데이터를 모았으니 이제 문제정의 먼저 해보겠습니다. 문제정의에 따라 데이터셋과 모델 구성이 달라지니 신중하게 생각할 부분입니다.
문제정의에 따라 데이터셋과 모델 구성이 달라진다.
갑자기 진지모드라 죄송합니다만 계속 이어가겠습니다. 주제가 “로또”인 것을 제외하고는 나름 딥러닝 입문자에게 도움이 될 부분이 많아서 중간중간에 설명이 포함되어 있습니다.
번호를 범주형으로
먼저 로또 번호에 대해서 살펴보겠습니다. 총 45개 번호 중에 6개 번호를 고르는 것입니다. 이런 용지에다가 사인펜으로 마킹을 하는 것이지요.
45개 번호라고 함은 1번에서 45번을 얘기하는 데, 각 번호들이 수치상의 의미가 있을까요? 또는 숫자들의 위치가 의미가 있을까요? 제가 보기에는 그냥 번호일뿐이지 수치나 위치상의 의미는 없어보입니다. 이를 어려운 단어로 “범주형 데이터”라고 합니다. 이런 범주형 데이터를 다루는 데 일반적으로 사용되는 기법이 “원핫인코딩”이 있습니다. 만약 1번에서 5번까지만 있다고 가정을 한다면 원핫인코딩은 각 번호를 아래와 같이 만듭니다.
- 1 : 10000
- 2 : 01000
- 3 : 00100
- 4 : 00010
- 5 : 00001
어렵지 않죠? 경우의 수만큼 0값을 가진 벡터를 만든다음 해당 자리수에 1로 설정하면 됩니다. 로또 번호인 경우에는 경우의 수가 45개이므로 아래와 같이 되겠네요.
- 01 : 100000000000000000000000000000000000000000000
- 02 : 010000000000000000000000000000000000000000000
- 03 : 001000000000000000000000000000000000000000000
- …
- 44 : 000000000000000000000000000000000000000000010
- 45 : 000000000000000000000000000000000000000000001
이렇게 구성하면 이제 로또 번호는 수치상의 의미를 가지는 것이 아닌 45개 경우의 수 중 하나인 클래스(범주)로 다루게 됩니다.
모델의 입출력 정의
장황하게 시작하고 있지만 모델 입출력은 간단합니다. 이전 회차의 당첨번호를 넣어서 다음회차의 당첨번호를 예측하는 것입니다.
이전회차 당첨번호 > |모델| > 다음회차 당첨번호 예측
그럼 이전회차 당첨번호를 어떻게 표현할까요? 45개 번호 중 6개가 당첨번호이니 45개의 벡터를 만들고 0으로 초기화한 뒤 이 중 당첨번호에 해당하는 벡터만 1로 설정해보도록 하죠. 앞서 원핫인코딩에 대해서 이해하셨고, 실제 로또 번호를 마킹하는 것과 비슷하니 크게 어려운 건 아닙니다. “벡터”의 개념은 그냥 “빈칸”이라고 생각하면 됩니다. “45개 벡터”는 “45개 빈칸”이라고 이해하면 되겠죠? 따라서 만약 이전회차 당첨번호가 “1,2,3,4,5,6”이라면 아래와 같이 벡터로 표시할 수 있습니다.
- 1,2,3,4,5,6 : 111111000000000000000000000000000000000000000
쉽죠? 45개의 빈칸에 1로 사이펜으로 마킹하는 것과 흡사합니다. 이를 함수로 만들면 아래와 같습니다. 원핫인코딩 값을 쉽게 확인 할 수 있도록 원핫인코딩을 번호로 변환하는 함수도 만들어봅니다.
import numpy as np
# 당첨번호를 원핫인코딩벡터(ohbin)으로 변환
def numbers2ohbin(numbers):
ohbin = np.zeros(45) #45개의 빈 칸을 만듬
for i in range(6): #여섯개의 당첨번호에 대해서 반복함
ohbin[int(numbers[i])-1] = 1 #로또번호가 1부터 시작하지만 벡터의 인덱스 시작은 0부터 시작하므로 1을 뺌
return ohbin
# 원핫인코딩벡터(ohbin)를 번호로 변환
def ohbin2numbers(ohbin):
numbers = []
for i in range(len(ohbin)):
if ohbin[i] == 1.0: # 1.0으로 설정되어 있으면 해당 번호를 반환값에 추가한다.
numbers.append(i+1)
return numbers
코드에 대한 부가 설명은 다음과 같습니다.
- ohbin은 one-hot encoding bin의 약자로 붙혀봤습니다. bin은 범주(카테고리) 벡터를 의미하는 용어인데, 어원은 잘 모르겠네요. 영상처리할 때 특징을 나타내는 벡터에서 자주쓰는 용어라 습관처럼 사용하게 되었습니다. 처음엔 ‘빈칸’에서 ‘빈’을 ‘bin’으로 표현한 줄 알았더니 외국에서도 사용하더군요. ㅎㅎ
- 벡터는 쉽게 배열로 생각하면 되는데, 배열의 인덱스는 항상 0부터 시작합니다. 비전공자분들이 자주 헷갈려하시는 부분입니다.
- 보너스 번호는 고려하지 않았습니다.
출력 또한 입력과 비슷하게 원핫인코딩 형태로 만듭니다. 그럼 실제 1회와 2회차를 예를 들어, 1회 당첨번호를 모델에 입력하면, 모델에서 2회 당첨번호를 알려준다고 가정을 해보죠. 먼저 1회, 2회차 당첨번호를 numbers2ohbin() 함수를 이용해서 ohbin으로 변환해봅니다.
print("1:" + str(numbers2ohbin([10,23,29,33,37,40])))
print("2:" + str(numbers2ohbin([9,13,21,25,32,42])))
1:[0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0.
0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 1. 0. 0. 0. 0. 0.]
2:[0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.
1. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
즉 아래처럼 1회차의 ohbin을 넣으면 2회차의 ohbin가 나오길 희망하는 것입니다.
000000000100000000000010000010001000100100000 > |모델| > 000000001000100000001000100000010000000001000
그럼 2회차의 ohbin을 얻어서 로또용지에 그대로 마킹하면 되겠죠?
샘플의 구성
샘플이라고 함은 지도학습(참고: 지도/비지도학습과 강화학습 풀이법) 문제에서 하나의 문제(X)와 정답(Y)의 한 쌍을 의미합니다. 따라서 이 경우 지도학습 모델의 입력이 문제가 되고, 모델의 출력의 정답이 됩니다. 샘플을 (X, Y)으로 표현했을 때, 우리가 만들 수 있는 샘플의 수는 총 893개입니다.
- (1회차 당첨번호, 2회차 당첨번호)
- (2회차 당첨번호, 3회차 당첨번호)
- (3회차 당첨번호, 4회차 당첨번호) …
- (892회차 당첨번호, 893회차 당첨번호)
- (893회차 당첨번호, 894회차 당첨번호)
앞서 수집한 데이터로부터 X와 Y로 구성된 샘플을 구성해보겠습니다. 먼저 파일을 로딩합니다. 1회차부터 894회차까지 있으므로 총 894개의 행이 존재함을 확인할 수 있습니다.
rows = np.loadtxt("./2020-1-25-keras_lstm_lotto_v895_data.csv", delimiter=",")
row_count = len(rows)
print("row count: " + str(row_count))
row count: 894
각 행에서 당첨번호만 추출하여 이를 원핫인코딩으로 변환한 뒤 앞서 언급한 샘플(X, Y)로 구성합니다. 샘플 중 가장 첫번째 샘플인 X가 1회차 당첨번호이고, Y가 2회차 당첨번호인 것만 확인해보겠습니다.
numbers = rows[:, 1:7]
ohbins = list(map(numbers2ohbin, numbers))
x_samples = ohbins[0:row_count-1]
y_samples = ohbins[1:row_count]
#원핫인코딩으로 표시
print("ohbins")
print("X[0]: " + str(x_samples[0]))
print("Y[0]: " + str(y_samples[0]))
#번호로 표시
print("numbers")
print("X[0]: " + str(ohbin2numbers(x_samples[0])))
print("Y[0]: " + str(ohbin2numbers(y_samples[0])))
ohbins
X[0]: [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0.
0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 1. 0. 0. 0. 0. 0.]
Y[0]: [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.
1. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
numbers
X[0]: [10, 23, 29, 33, 37, 40]
Y[0]: [9, 13, 21, 25, 32, 42]
데이터셋 구성
샘플로부터 데이터셋을 구성해보겠습니다. 데이터셋 구성에 대해서 처음해보신 분은 먼저 데이터셋 이야기를 읽어보시는 것을 추천드립니다. 그럼 우린 배운데로 “훈련셋/검증셋/시험셋”으로 나누어보겠습니다.
- 훈련셋: (1회 입력, 2회 출력)부터 (700회 입력, 701회)까지 700개 샘플
- 검증셋: (701회, 702회)부터 (800회, 801회)까지 100개 샘플
- 시험셋: (801회, 802회)부터 (893회, 894회)까지 93개 샘플
이렇게 나누는 기준은 딱히 정해진 것은 없지만 데이터수가 적으므로 위와 같이 지정했습니다.
train_idx = (0, 700)
val_idx = (700, 800)
test_idx = (800, len(x_samples))
print("train: {0}, val: {1}, test: {2}".format(train_idx, val_idx, test_idx))
train: (0, 700), val: (700, 800), test: (800, 893)
모델 구성
모델을 딥러닝 라이브러리 중 하나인 텐서플로우 2.0의 케라스를 이용합니다. 구글 코랩에서 시작하시는 분은 아래 명령을 통해서 텐서플로우 2.0을 설치합니다.
from __future__ import absolute_import, division, print_function, unicode_literals
!pip install tensorflow-gpu==2.0.0-rc1
Collecting tensorflow-gpu==2.0.0-rc1
[?25l Downloading https://files.pythonhosted.org/packages/73/cf/2fc69ba3e59edc8333e2676fa71b40197718dea7dc1282c79955cf6b2acb/tensorflow_gpu-2.0.0rc1-cp36-cp36m-manylinux2010_x86_64.whl (380.5MB)
[K |████████████████████████████████| 380.5MB 37kB/s
...
Installing collected packages: tb-nightly, tf-estimator-nightly, tensorflow-gpu
Successfully installed tb-nightly-1.15.0a20190806 tensorflow-gpu-2.0.0rc1 tf-estimator-nightly-1.14.0.dev2019080601
모델은 간단하게 상태유지 LSTM 모델로 구성해봅니다. 몇가지 특징을 나열해봤습니다.
- 타입스텝은 1인 대신, 상태유지(stateful 옵션을 True)으로 설정했습니다.
- 45개의 벡터로 출력합니다.
- 각각의 벡터는 0.0과 1.0사이의 실수값으로 나옵니다. 각 벡터가 독립적으로 모두 1.0이 나오거나 0.0이 나올 수 있는 멀티레이블 문제입니다.
- 멀티레이블 문제라 출력층의 활성화함수가 softmax가 아닌 sigmoid로 설정하였습니다.
모델 소스코드는 간단하지만 모델 이해를 위한 선행지식을 원하시는 분들은 아래 링크를 참고하세요.
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import models
# 모델을 정의합니다.
model = keras.Sequential([
keras.layers.LSTM(128, batch_input_shape=(1, 1, 45), return_sequences=False, stateful=True),
keras.layers.Dense(45, activation='sigmoid')
])
# 모델을 컴파일합니다.
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
모델 학습
모델 컴파일까지 완료했다면 훈련셋으로 모델을 학습시킵니다. 모델을 학습시키는 코드는 “model.train_on_batch()” 코드 한 줄이지만 학습과정을 살펴보는 것이 중요하므로 부가 코드들이 삽입되어 있습니다. 또한 과적합이 일어나지 않은 최적의 학습 모델을 얻는 것이 목표이므로 매 에포크마다 학습된 모델을 파일로 저장하는 코드도 삽입되어 있습니다.
부가 코드들에 대해서 좀 더 살펴보시고 싶다면 아래 링크를 참고하세요.
# 매 에포크마다 훈련과 검증의 손실 및 정확도를 기록하기 위한 변수
train_loss = []
train_acc = []
val_loss = []
val_acc = []
# 최대 100번 에포크까지 수행
for epoch in range(100):
model.reset_states() # 중요! 매 에포크마다 1회부터 다시 훈련하므로 상태 초기화 필요
batch_train_loss = []
batch_train_acc = []
for i in range(train_idx[0], train_idx[1]):
xs = x_samples[i].reshape(1, 1, 45)
ys = y_samples[i].reshape(1, 45)
loss, acc = model.train_on_batch(xs, ys) #배치만큼 모델에 학습시킴
batch_train_loss.append(loss)
batch_train_acc.append(acc)
train_loss.append(np.mean(batch_train_loss))
train_acc.append(np.mean(batch_train_acc))
batch_val_loss = []
batch_val_acc = []
for i in range(val_idx[0], val_idx[1]):
xs = x_samples[i].reshape(1, 1, 45)
ys = y_samples[i].reshape(1, 45)
loss, acc = model.test_on_batch(xs, ys) #배치만큼 모델에 입력하여 나온 답을 정답과 비교함
batch_val_loss.append(loss)
batch_val_acc.append(acc)
val_loss.append(np.mean(batch_val_loss))
val_acc.append(np.mean(batch_val_acc))
print('epoch {0:4d} train acc {1:0.3f} loss {2:0.3f} val acc {3:0.3f} loss {4:0.3f}'.format(epoch, np.mean(batch_train_acc), np.mean(batch_train_loss), np.mean(batch_val_acc), np.mean(batch_val_loss)))
model.save('model_{0:04d}.h5'.format(epoch+1))
WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow_core/python/ops/math_grad.py:1394: where (from tensorflow.python.ops.array_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where
epoch 0 train acc 0.862 loss 0.410 val acc 0.867 loss 0.397
epoch 1 train acc 0.867 loss 0.396 val acc 0.867 loss 0.397
epoch 2 train acc 0.867 loss 0.394 val acc 0.867 loss 0.396
epoch 3 train acc 0.867 loss 0.392 val acc 0.867 loss 0.397
epoch 4 train acc 0.867 loss 0.388 val acc 0.867 loss 0.398
...
epoch 91 train acc 0.999 loss 0.011 val acc 0.811 loss 1.203
epoch 92 train acc 0.999 loss 0.009 val acc 0.817 loss 1.189
epoch 93 train acc 1.000 loss 0.007 val acc 0.811 loss 1.178
epoch 94 train acc 1.000 loss 0.007 val acc 0.811 loss 1.198
epoch 95 train acc 0.996 loss 0.016 val acc 0.805 loss 1.174
epoch 96 train acc 0.993 loss 0.026 val acc 0.807 loss 1.204
epoch 97 train acc 0.998 loss 0.014 val acc 0.813 loss 1.231
epoch 98 train acc 0.998 loss 0.011 val acc 0.814 loss 1.216
모델 학습 과정 살펴보기
매 에포크마다 저장된 훈련셋의 손실값 및 정확도와 검증셋의 손실값 및 정확도에 대해서 기록한 것을 그래프로 표현해봤습니다.
%matplotlib inline
import matplotlib.pyplot as plt
fig, loss_ax = plt.subplots()
acc_ax = loss_ax.twinx()
loss_ax.plot(train_loss, 'y', label='train loss')
loss_ax.plot(val_loss, 'r', label='val loss')
acc_ax.plot(train_acc, 'b', label='train acc')
acc_ax.plot(val_acc, 'g', label='val acc')
loss_ax.set_xlabel('epoch')
loss_ax.set_ylabel('loss')
acc_ax.set_ylabel('accuray')
loss_ax.legend(loc='upper left')
acc_ax.legend(loc='lower left')
plt.show()
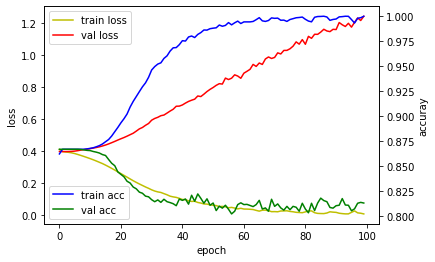
정상적으로 학습할 수 있는 일반적인 데이터셋과 모델이라면 val loss(빨간색)이 떨어지다가 다시 올라가는 것이 정상입니다. 즉 훈련을 하면서 검증셋에 대해서도 잘 맞추다가 어느정도 훈련이 진행되면 검증셋의 손실값(val loss)를 다시 올라갑니다. 우리는 이 시점을 과적합(오버피팅)이 되었다고 하고, 이 시점 이전의 저장된 모델을 사용하는 것이 일반적입니다.
하지만 보시다시피 학습이 시작하자마다 검증셋의 손실값이 올라갑니다. 이 말은 처음에 그냥 랜덤인 상태가 차라리 더 좋다는 것이고 학습이 진행되면 바로 오버피팅이 일어나서 오히러 결과가 더 좋지 않다는 것을 의미합니다. 이 그래프를 통해 다시금 깨닫게 됩니다.
로또는 독립시행이라 이전 번호로 학습하는 것이 무의미하다.
이 그래프를 보는 순간 이후 과정은 사실 무의미하지만 본 글은 교육의 목적이 있으므로 그래도 끝까지 가보겠습니다.
모델 검증
모델을 검증하는 방법은 여러가지가 있을 수 있습니다. 1등 당첨번호를 잘 맞추는 것도 중요하지만 로또 시스템은 등수별로 차등으로 상금이 주어지기 때문에 등수를 낮더라도 상금을 타는 확률을 높이는 것이 더 좋을 수도 있습니다. 학습한 모델을 등수와 상금 관점에서 얼마나 잘 맞는 지 검증을 해보도록 하겠습니다.
메트릭 추가
지난 회차인 경우 각 회차마다 등수별 상금이 정해져 있긴 하지만 1등이 나오지 않는 결측치도 있고, 87회차 이전까지는 한 판의 가격이 2천원이어서 이를 아래와 같이 간소화 시켰습니다.
- 한 판의 가격은 1천원이다
- 88회차부터 지금까지 1등부터 5등까지의 등수별로 평균낸다
# 88회부터 지금까지 1등부터 5등까지 상금의 평균낸다.
mean_prize = [ np.mean(rows[87:, 8]),
np.mean(rows[87:, 9]),
np.mean(rows[87:, 10]),
np.mean(rows[87:, 11]),
np.mean(rows[87:, 12])]
print(mean_prize)
[2434854568.0359354, 57192272.95167286, 1451891.8711276331, 53061.93060718711, 5000.0]
그리고 예측한 번호를 당첨번호와 보너스번호와 함께 입력하면 등수 및 평균 상금을 반환해주는 함수가 필요하겠네요.
# 등수와 상금을 반환함
# 순위에 오르지 못한 경우에는 등수가 0으로 반환함
def calc_reward(true_numbers, true_bonus, pred_numbers):
count = 0
for ps in pred_numbers:
if ps in true_numbers:
count += 1
if count == 6:
return 0, mean_prize[0]
elif count == 5 and true_bonus in pred_numbers:
return 1, mean_prize[1]
elif count == 5:
return 2, mean_prize[2]
elif count == 4:
return 3, mean_prize[3]
elif count == 3:
return 4, mean_prize[4]
return 5, 0
즉 우리는 모델 검증하기 위해 두 가지 메트릭을 추가한 셈입니다. 즉 이는 다음의 의미를 내포하고 있습니다.
당첨번호를 맞추는 것도 중요하지만 몇 등인지 상금이 얼마인지도 중요하다
그럼 실제 로또 번호를 생성해보도록 하죠. 모델 출력은 45개의 0.0과 1.0사이의 값으로 나오는 1차원 벡터입니다. 각 번호에 할당된 벡터의 값이 1.0에 가까울수록 모델이 생각하기에 당첨확률이 높은 번호이고 0.0에 가까울수록 당첨확률이 낮은 번호입니다. 따라서 모델 출력에서 가장 확률값이 높은 6개의 벡터를 구하면 그것이 모델이 예측하는 당첨번호라고 볼 수 있습니다. 보통 10판씩(1만원)을 하는 데, 당첨번호를 한 개 받아서 같은 번호로 10판하는 것은 리스크가 있어보이므로 서로 다른 번호들로 10판을 구성하는 것이 더 나아보입니다. 기분만 그런 것 뿐이지 통계상으론 크게 의미가 없을겁니다. 제가 모델 출력으로부터 번호를 생성하는 방식은 다음과 같습니다.
. 45개의 벡터마다 출력값을 가져온다. 각 벡터의 출력값은 0.0에서 1.0이다. *. 각 벡터마다 벡터의 출력값에 100을 곱한 뒤 1을 더한 값만큼의 수만큼 해당 번호의 공을 만든다. * 즉 0번째 벡터(번호 1번)의 값이 0.2이었다면, 1번 공을 21개(0.2100+1) 만든다. * 즉 7번째 벡터(번호 8번)의 값이 0.0이었다면, 8번 공을 1개(0.0100+1) 만든다. * 즉 40번째 벡터(번호 41번)의 값이 0.99이었다면, 41번 공을 100개(0.99100+1) 만든다. *. 만든 공을 큰 박스에 담는다.
- 박스에서 하나를 고른 후 다시 박스에 담는다.
- 고른 번호가 이전에 고른 번호가 아니라면 추천번호로 저장한다. 만약 이미 고른 번호라면 다시 하나를 고른 뒤 박스에 담는다. *. 추천번호가 6개가 될 때까지 위 과정을 반복한다.
이런 식으로 번호를 생성하면, 모델의 해당 번호의 벡터 출력값이 높을 수록 그 번호의 공의 개수가 늘어납니다. 특정 번호의 공 개수가 많다고 해서 반드시 박스에서 뽑히지는 않고, 또한 공의 개수가 하나라고 안 뽑히는 것도 아니므로 적당히 10개의 로또 번호가 다르게 나올 수 있습니다. 이렇게 번호를 뽑는 함수를 “gen_numbers_from_probability()”으로 만들어봤습니다.
def gen_numbers_from_probability(nums_prob):
ball_box = []
for n in range(45):
ball_count = int(nums_prob[n] * 100 + 1)
ball = np.full((ball_count), n+1) #1부터 시작
ball_box += list(ball)
selected_balls = []
while True:
if len(selected_balls) == 6:
break
ball_index = np.random.randint(len(ball_box), size=1)[0]
ball = ball_box[ball_index]
if ball not in selected_balls:
selected_balls.append(ball)
return selected_balls
이제 학습한 모델도 있고, 모델 결과로부터 번호를 생성하는 함수도 있고, 그렇게 생성한 번호로부터 등수와 상금을 계산하는 함수도 있습니다. 그럼 실험을 해볼까요?
실험은 입력을 1회차부터 893회차까지 해보겠습니다. 즉
- 1회차 당첨번호를 모델에 입력한 후 모델 출력으로부터 10판의 번호를 생성한 뒤 2회차와 비교하여 등수와 상금 계산
- 2회차 당첨번호를 모델에 입력한 후 모델 출력으로부터 10판의 번호를 생성한 뒤 3회차와 비교하여 등수와 상금 계산
- …
- 893회차 당첨번호를 모델에 입력한 후 모델 출력으로부터 10판의 번호를 생성한 뒤 894회차와 비교하여 등수와 상금 계산
모델을 1회차부터 다시 추론을 해야하므로 상태 초기화부터 시작합니다. 실험 코드는 아래와 같습니다.
train_total_reward = []
train_total_grade = np.zeros(6, dtype=int)
val_total_reward = []
val_total_grade = np.zeros(6, dtype=int)
test_total_reward = []
test_total_grade = np.zeros(6, dtype=int)
model.reset_states()
print('[No. ] 1st 2nd 3rd 4th 5th 6th Rewards')
for i in range(len(x_samples)):
xs = x_samples[i].reshape(1, 1, 45)
ys_pred = model.predict_on_batch(xs) # 모델의 출력값을 얻음
sum_reward = 0
sum_grade = np.zeros(6, dtype=int) # 6등까지 변수
for n in range(10): # 10판 수행
numbers = gen_numbers_from_probability(ys_pred[0])
#i회차 입력 후 나온 출력을 i+1회차와 비교함
grade, reward = calc_reward(rows[i+1,1:7], rows[i+1,7], numbers)
sum_reward += reward
sum_grade[grade] += 1
if i >= train_idx[0] and i < train_idx[1]:
train_total_grade[grade] += 1
elif i >= val_idx[0] and i < val_idx[1]:
val_total_grade[grade] += 1
elif i >= test_idx[0] and i < test_idx[1]:
val_total_grade[grade] += 1
if i >= train_idx[0] and i < train_idx[1]:
train_total_reward.append(sum_reward)
elif i >= val_idx[0] and i < val_idx[1]:
val_total_reward.append(sum_reward)
elif i >= test_idx[0] and i < test_idx[1]:
test_total_reward.append(sum_reward)
print('[{0:4d}] {1:3d} {2:3d} {3:3d} {4:3d} {5:3d} {6:3d} {7:15,d}'.format(i+1, sum_grade[0], sum_grade[1], sum_grade[2], sum_grade[3], sum_grade[4], sum_grade[5], int(sum_reward)))
print('Total')
print('==========')
print('Train {0:5d} {1:5d} {2:5d} {3:5d} {4:5d} {5:5d} {6:15,d}'.format(train_total_grade[0], train_total_grade[1], train_total_grade[2], train_total_grade[3], train_total_grade[4], train_total_grade[5], int(sum(train_total_reward))))
print('Val {0:5d} {1:5d} {2:5d} {3:5d} {4:5d} {5:5d} {6:15,d}'.format(val_total_grade[0], val_total_grade[1], val_total_grade[2], val_total_grade[3], val_total_grade[4], val_total_grade[5], int(sum(val_total_reward))))
print('Test {0:5d} {1:5d} {2:5d} {3:5d} {4:5d} {5:5d} {6:15,d}'.format(test_total_grade[0], test_total_grade[1], test_total_grade[2], test_total_grade[3], test_total_grade[4], test_total_grade[5], int(sum(test_total_reward))))
print('==========')
[No. ] 1st 2nd 3rd 4th 5th 6th Rewards
[ 1] 4 0 6 0 0 0 9,748,129,623
[ 2] 3 0 6 1 0 0 7,313,328,117
[ 3] 4 0 5 1 0 0 9,746,730,793
[ 4] 6 0 4 0 0 0 14,614,934,975
[ 5] 6 0 2 1 1 0 14,612,089,253
[ 6] 4 0 2 4 0 0 9,742,534,303
...
[ 695] 0 1 7 1 1 0 67,413,577
[ 696] 2 0 6 1 1 0 4,878,478,549
[ 697] 0 0 7 3 0 0 10,322,428
[ 698] 4 0 4 2 0 0 9,745,331,963
[ 699] 1 1 4 4 0 0 2,498,066,656
[ 700] 2 2 4 2 0 0 4,990,007,373
[ 701] 0 0 0 0 0 10 0
[ 702] 0 0 0 0 0 10 0
[ 703] 0 0 0 0 3 7 15,000
[ 704] 0 0 0 0 1 9 5,000
[ 705] 0 0 0 0 0 10 0
...
[ 891] 0 0 0 0 0 10 0
[ 892] 0 0 0 0 0 10 0
[ 893] 0 0 0 0 0 10 0
Total
==========
Train 2561 81 3282 963 106 7 6,245,111,860,609
Val 0 0 0 3 54 1873 190,000
Test 0 0 0 0 0 0 239,185
==========
모델의 검증은 하나의 매트릭으로만 하는 것이 아니라 여러가지 매트릭이 적용됩니다. 여기서는 정확도뿐만아니라 상금의 척도 사용한 것입니다. 결국 우리가 원하는 것인 상금이니깐요. 그럼 우리가 학습한 모델의 결과를 2회차부터 지금까지 추론하였을 때 상금이 얼마인지 그래프로 표시해볼까요?
%matplotlib inline
import matplotlib.pyplot as plt
total_reward = train_total_reward + val_total_reward + test_total_reward
plt.plot(total_reward)
plt.ylabel('rewards')
plt.show()
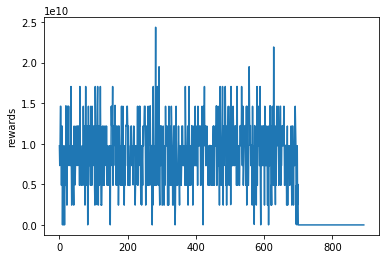
701번째부터 상금이 뚝 떨어졌죠? 즉 700번째까지는 이미 학습(이라부르지만 거의 외움)한 것이라 1등도하고 2등도 하고 3등도 하고 하지만, 701번째부터는 학습을 하지 않은 샘플인데, 상금도 거의 없습니다. 즉 로또는 학습해서 될 문제가 아니라는 것이죠. 제가 대신 하는 것으로 대리만족 부탁드립니다. 훈련셋, 검증셋, 시험셋으로 상금을 막대그래프로 표시해봤습니다. val과 test 상금이 train 상금보다 적어서 막대로 표시도 안되네요.
%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
ax = plt.figure().gca()
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
rewards = [sum(train_total_reward), sum(val_total_reward), sum(test_total_reward)]
class_color=['green', 'blue', 'red']
plt.bar(['train', 'val', 'test'], rewards, color=class_color)
plt.ylabel('rewards')
plt.show()

시계열 데이터에서의 학습과 검증
시계열 데이터에서의 학습과 검증은 데이터셋을 나누는 데에 있어서 조금 더 신경써야할 것이 있습니다.
앞서 원주율을 예를 들었는 데, 다시 보겠습니다.
- 학습과정
- 3 > 1
- 3.1 > 4
- 3.14 > 1
- 3.141 > 5
- …
- 3.141592653589793238462643383279502884 > 1
- 추론과정
- 3.1415926535897932384626433832795028841 > 9(희망)
즉 우리가 원하는 추론과정은 마지막 “9”을 추론하는 것이지 그 이상을 추론하는 것이 아닙니다. 즉 “9”를 추론하기 위에서 그 직전까지 학습시키고, 그 다음 한 스텝만 추론하면 됩니다. 하지만 우리는 앞서 아래와 같이 나누었습니다.
- 훈련셋: (1회 입력, 2회 출력)부터 (700회 입력, 701회 출력)까지 700개 샘플
- 검증셋: (701회 입력, 702회)부터 (800회 입력, 801회 출력)까지 100개 샘플
- 시험셋: (801회 입력, 802회)부터 (893회 입력, 894회 출력)까지 93개 샘플
즉 검증셋과 시험셋을 추론할 때, 1회 입력, 2회 출력)부터 (700회 입력, 701회 출력)까지 700개 샘플만 학습한 것을 가지고 100개 + 93개를 추론한 것입니다. 사실 우리는 다음회차 로또 번호를 예측하기 위해서, 직전까지만 학습한 것을 가지고 하나의 타임스텝만을 추론하면 되므로, 여기에 맞는 검증 방법과 시험 방법이 필요합니다. 특히 검증 방법이 중요한데요, 이러한 시계열 데이터에서 한 스텝을 예측하는 문제는 walk-forward model validation 방법을 사용해야 합니다. 이 부분에서는 다음회차에서 다루겠습니다. 이번에는 (사실 검증하는 것이 별로 의미가 없으므로 우주의 기운만 넣어봐요) 894회차까지 번호를 다 학습시키고, 마지막 895회차만 예측해보겠습니다. 사실 검증셋을 이용해서 하이퍼파라미터 튜닝을 해야하지만, 이것도 다음 회차에서 적용해보도록 하겠습니다.
# 최대 100번 에포크까지 수행
for epoch in range(100):
model.reset_states() # 중요! 매 에포크마다 1회부터 다시 훈련하므로 상태 초기화 필요
for i in range(len(x_samples)):
xs = x_samples[i].reshape(1, 1, 45)
ys = y_samples[i].reshape(1, 45)
loss, acc = model.train_on_batch(xs, ys) #배치만큼 모델에 학습시킴
batch_train_loss.append(loss)
batch_train_acc.append(acc)
train_loss.append(np.mean(batch_train_loss))
train_acc.append(np.mean(batch_train_acc))
print('epoch {0:4d} train acc {1:0.3f} loss {2:0.3f}'.format(epoch, np.mean(batch_train_acc), np.mean(batch_train_loss)))
epoch 0 train acc 0.974 loss 0.131
epoch 1 train acc 0.955 loss 0.181
epoch 2 train acc 0.952 loss 0.183
...
epoch 97 train acc 0.991 loss 0.033
epoch 98 train acc 0.992 loss 0.033
epoch 99 train acc 0.992 loss 0.032
# 마지막 회차까지 학습한 모델로 다음 회차 추론
print('receive numbers')
xs = x_samples[-1].reshape(1, 1, 45)
ys_pred = model.predict_on_batch(xs)
list_numbers = []
for n in range(10):
numbers = gen_numbers_from_probability(ys_pred[0])
print('{0} : {1}'.format(n, numbers))
list_numbers.append(numbers)
receive numbers
0 : [26, 12, 23, 44, 31, 6]
1 : [26, 43, 12, 31, 3, 41]
2 : [40, 44, 20, 12, 26, 41]
3 : [26, 24, 40, 31, 7, 12]
4 : [12, 26, 23, 43, 31, 41]
5 : [31, 27, 43, 26, 5, 28]
6 : [41, 40, 26, 23, 34, 43]
7 : [23, 41, 12, 40, 43, 39]
8 : [26, 40, 31, 12, 23, 41]
9 : [31, 26, 41, 43, 40, 44]
실제 로또 구매
가장 중요한 단계입니다. 케라스 모델을 통해서 받은 번호로 실제로 (용기내어) 사보는 것입니다.

실제 로또 추첨 결과
1만원(10판)을 투자하여 895 회차를 추첨한 결과 5천원이 4번 당첨되어 총 상금이 2만원입니다. 첫 시작으로는 나쁘지 않은 결과입니다.
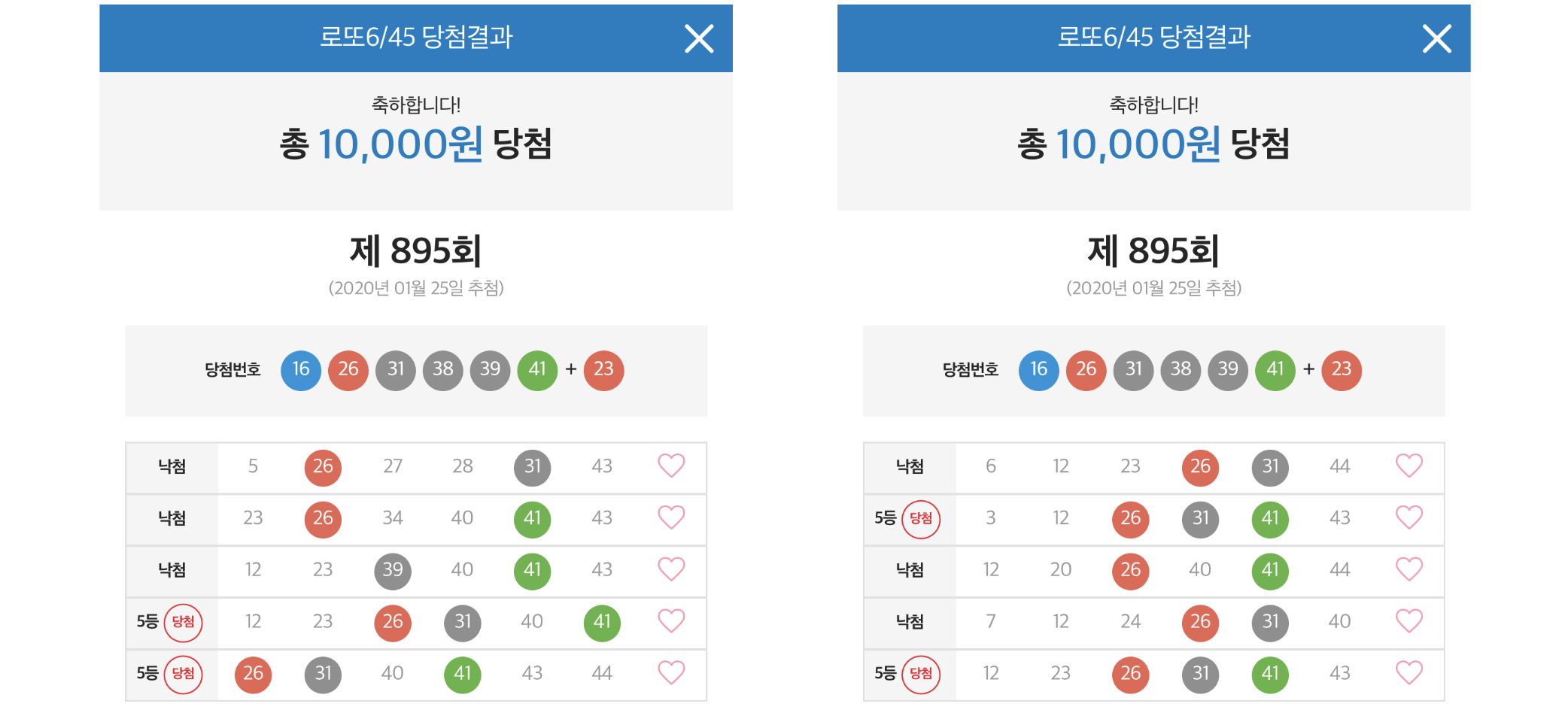
혹시 당첨이후에 쓴 글이라 조작이라고 생각하시는 분들을 위해, 로또 당첨 전에 추론한 모델 소스코드 및 실행 결과를 저장한 링크를 첨부했습니다.
- 링크: https://gist.github.com/tykimos/e792fcae92de2326e273d669d652366b
향후 계획
다음 회차들에서는 아래의 기법들을 적용해볼 예정입니다.
- 추첨번호 오름차순으로 출력
- walk-forwad model validation을 이용한 검증 및 하아피파라미터 튜닝
- label smoothing 기법 적용
- 손실함수 정의 시 class weight 고려
- 회차 정보 삽입
- 각종 통계치 및 패턴(CNN) 피처 추가
많은 기법들이 적용되는 것이 이번 문제에서는 큰 의미가 없으나 교육 자료로는 해볼만 합니다.
책 소개

[추천사]
- 하용호님, 카카오 데이터사이언티스트 - 뜬구름같은 딥러닝 이론을 블록이라는 손에 잡히는 실체로 만져가며 알 수 있게 하고, 구현의 어려움은 케라스라는 시를 읽듯이 읽어내려 갈 수 있는 라이브러리로 풀어준다.
- 이부일님, (주)인사아트마이닝 대표 - 여행에서도 좋은 가이드가 있으면 여행지에 대한 깊은 이해로 여행이 풍성해지듯이 이 책은 딥러닝이라는 분야를 여행할 사람들에 가장 훌륭한 가이드가 되리라고 자부할 수 있다. 이 책을 통하여 딥러닝에 대해 보지 못했던 것들이 보이고, 듣지 못했던 것들이 들리고, 말하지 못했던 것들이 말해지는 경험을 하게 될 것이다.
- 이활석님, 네이버 클로바팀 - 레고 블럭에 비유하여 누구나 이해할 수 있게 쉽게 설명해 놓은 이 책은 딥러닝의 입문 도서로서 제 역할을 다 하리라 믿습니다.
- 김진중님, 야놀자 Head of STL - 복잡했던 머릿속이 맑고 깨끗해지는 효과가 있습니다.
- 이태영님, 신한은행 디지털 전략부 AI LAB - 기존의 텐서플로우를 활용했던 분들에게 바라볼 수 있는 관점의 전환점을 줄 수 있는 Mild Stone과 같은 책이다.
- 전태균님, 쎄트렉아이 - 케라스의 특징인 단순함, 확장성, 재사용성을 눈으로 쉽게 보여주기 위해 친절하게 정리된 내용이라 생각합니다.
- 유재준님, 카이스트 - 바로 적용해보고 싶지만 어디부터 시작할지 모를 때 최선의 선택입니다.